
2.选用课时作业优化设计.
1.课本P60习题14.2第4,5,6题.
此课时是运用勾股定理和判定直角三角形的勾股逆定理来解决实际问题,解决这类问题的关键是画出正确的图形,通过数形结合,构造直角三角形,碰到空间曲面上两点间的最短距离间题,一般是化空间问题为平面问题来解决.即将空间曲面展开成平面,然后利用勾
股定理及相关知识进行求解,遇到求不规则面积问题,通常应用化归思想,将不规则问
题转换成规则何题来解决.解题中,注意辅助线的使用.特别是“经验辅助线”的使用.
课本P60练习第1,2题
例3 如图14.2.5,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:
(1) 从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为22;
(2) 画出所有的以(1)中的AB为边的等腰三角形, 使另一个顶点在格点上,且另两边的长度都是无理数.
教师分析 只需利用勾股定理看哪一个矩形的对角线满足要求.
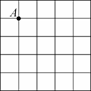
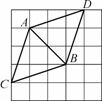
图14.2.5 图14.2.6
解(1) 图14.2.6中AB长度为22.
(2) 图14.2.6中△ABC、 △ABD就是所要画的等腰三角形.
学生活动:参与例3的学习 ,动手画图,交流、讨论,弄清理由
例4如图14.2.7,已知CD=6m, AD=8m, ∠ADC=90°, BC=24m, AB=26m.求图中阴影部分的面积.
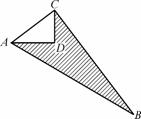
图14.2.7
教师分析:课本图14.2.7中阴影部分的面积是一个不规则的图形,因此我们首先应考虑如何转化为规则图形的和差形,这是方向,同学们记住,实际上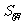 =
= -
-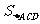 ,现在只要明确怎样计算
,现在只要明确怎样计算 和
和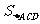 了。
解 在Rt△ADC中,
了。
解 在Rt△ADC中,
AC =AD
=AD +CD
+CD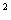 =6
=6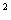 +8
+8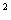 =100(勾股定理),
=100(勾股定理),
∴ AC=10m.
∵ AC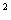 +BC
+BC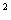 =10
=10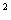 +24
+24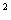 =676=AB
=676=AB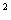
∴ △ACB为直角三角形(如果三角形的三边长a、 b、 c有关系: a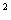 +b
+b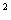 =c
=c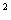 ,那么这个三角形是直角三角形),
,那么这个三角形是直角三角形),
∴ S阴影部分=S△ACB-S△ACD
=1/2×10×24-1/2×6×8=96(m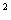 ).
).
评析:这题应总结出两种思想方法:一是求不规则图形的面积方法“将不规则图化成规则”,二是求面积中,要注意其特殊性.
学生活动:参与讲例,积极思考,提出自己的看法,归纳总结解题思路
教师道白:在一棵树的l0m高的D处有两只猴子,其中一只猴子爬下树走到离树
20m处的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的距
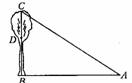 离相等,试问这棵树有多高?
离相等,试问这棵树有多高?
评析:如图所示,其中一只猴子从D→B→A共走了30m,另一只猴子从D→C→A也共走了30m,且树身垂直于地面,于是这个问题可化归到直角三角形解决.
教师活动操作投影仪,提出问题,引导学生分析问题、明确题意,用化归的思想解决问题.
学生活动:积极思考,讨论,运用数学手段来理出思路,解决问题
解:设DC=xm,依题意得:BD+BA=DC+CA
CA=30-x,BC=l0+x
在RtnABC中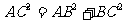 AC' =AB' +BC
AC' =AB' +BC
即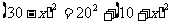
解之x=5
所以树高为15m.
媒体使用:投影显示.
P60页习题14.2第1,2,3,4题
由学生分小组进行总结,教师请个别组学生在全班总结勾定理的应用方法.
 (1)如果剪4刀,应如何剪拼?
(1)如果剪4刀,应如何剪拼?
(2)少剪几刀,也能拼成一个大正方形吗?
教师活动:操作投影仪,引导学生动手操作,感受方法.
学生活动分小组合作交流,得到答案.
教师活动:操作投影仪,提出问题,引导学生思考.
学生活动:先独立解题,再踊跃上台演示.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com