1. 在三角形ABC中，h是底边a上的高，当a为定长时，在三角形面积S=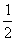ah中，常量是　　　　　 变量　　　　

2　　　　 在匀速直线运动中，当S一定时，速度V与时间t的关系式是　　　　　　

3　　　　 向一个空水箱内注水，每分钟注水5升，则水箱内水量Q(升)与注水时间t(分)之间m 关系式　　　　　　　　

27．解：把x＝1代入原方程并整理得(b+4)k＝7－2a

要使等式(b+4)k＝7－2a不论k取什么实数均成立，只有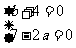

26．解：(1)当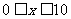时，设抛物线的函数关系式为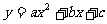，由于它的图象经过点(0，20)，(5，39)，(10，48)，所以

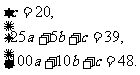
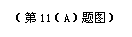解得，，，.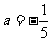

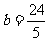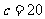所以

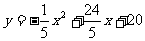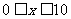，.　 …………………(5分)

(2)当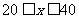时，.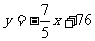

所以，当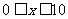时，令y=36，得，

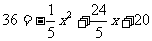解得x=4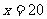，(舍去)；

当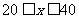时，令 y=36，得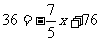，解得

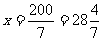.　　　　　 ……………………(10分)

因为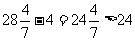，所以，老师可以经过适当的安排，在学生注意力指标数不低于36时，讲授完这道竞赛题.　　　　　　　 ……………………(15分)

25．解(1)由题设知，A市、B市、C市发往D市的机器台数分x，x，18-2x，发往E市的机器台数分别为10-x，10-x，2x-10．于是

W=200x+300x+400(18-2x)+800(10-x)+700(10-x)+500(2x-10)

=-800x+17200．

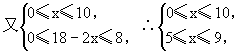
∴5≤x≤9．

∴W=-800x+17200(5≤x≤9，x是整数)

由上式可知，W是随着x的增加而减少的，所以当x=9时，W取到最小值10000元；当x=5时，W取到最大值13200元．

(2)由题设知，A市、B市、C市发往D市的机器台数分别为x，y，18-x-y，发往E市的机器台数分别是10-x，10-y，x+y-10，于是

W=200x+800(10-x)+300y+700(10-y)+400(19-x-y)+500(x+y-10)

=-500x-300y-17200

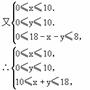
∴W=-500x-300y+17200，

W=-200x-300(x+y)+17200

≥-200×10-300×18+17200=9800．

当x=10，y=8时，W=9800．所以，W的最小值为9800．

又W=-200x-300(x+y)+17200

≤-200×0-300×10+17200=14200．

当x=0，y=10时，W=14200，所以，W的最大值为14200．

24．解：设每月用水量为x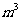，支付水费为y元。则

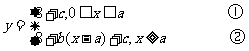
由题意知：0＜c≤5　　　 ∴ 0＜8+c≤13

从表中可知，第二、三月份的水费均大于13元，故用水量15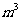、22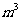均大于最低限量a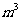，将x＝15，x＝22分别代入②式，得

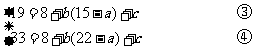
解得　 b＝2，　2a＝c+19　　　⑤

再分析一月份的用水量是否超过最低限量，不妨设9＞a，将x＝9代入②，得

9＝8+2(9－a)+c，即2a＝c+17　 ⑥

⑥与⑤矛盾。

故9≤a，则一月份的付款方式应选①式，则8+c＝9，　∴　c＝1

代入⑤式得，a＝10。

综上得　a＝10，b＝2，c＝1。

23．(1)2个n,24和48；

　　 (2)最少302元，最多384元。

22．(1)设预计购买甲、乙商品的单价分别为a元和b元，则原计划是：

　ax+by=1500，　①

　由甲商品单价上涨1.5元，乙商品单价上涨1元，并且甲商品减少10个情形，得：

　(a+1.5)(x-10)+(b+1)y=1529.　②

　再由甲商品单价上涨1元，而数量比预计数少5个，乙商品单价上涨仍是1元的情形得：

　(a+1)(x-5)+(b+1)y=1563.5.　③

　由①，②，③得：

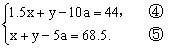
　④-⑤×2并化简，得x+2y=186.

　(2)依题意有：

　205＜2x+y＜210及x+2y=186.

　得54＜y＜.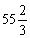

　由于y是整数，得y=55，从而得x=76.

21．　解：

　(1)按优惠方案①可得

　　y₁=20×4+(x-4)×5=5x+60(x≥4) 　…………2分

　　按优惠方案②可得

　　y₂=(5x+20×4)×92%=4.6x+73.6(x≥4) 　…………4分

　(2)比较

　　y₁-y₁=0.4x-13.6(x≥4)

　　令y₁-y₁=0，得x=34　…………7分

　　∴当购买34盒水彩时，两种优惠方案付款一样多。　…………8分

　　当4≤x<34时，y₁<y₂，优惠方案①付款较少。　…………9分

　　当x>34时，y₁>y₂，优惠方案②付款较少。　…………10分

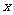　∵＞7104＞400

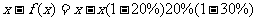∴………………………7分

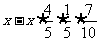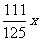＝＝＝7104……………………9分

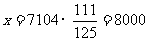∴(元)

答：这笔稿费是8000元。………………………………………………12分

20．(1)y=-x+180 (0＜x＜180)

　　 (2)3500≤w≤4200

18．(2)