
3.计算(-5ax)·(3x2y)2的结果是( )
A.-45ax5y2 B.-15ax5y2 C.-45x5y2 D.45ax5y2
2.下列计算的结果正确的是( )
A.(-x2)·(-x)2=x4 B.x2y3·x4y3z=x8y9z
C.(-4×103)·(8×105)=-3.2×109 D.(-a-b)4·(a+b)3=-(a+b)7
1.式子x4m+1可以写成( )
A.(xm+1)4 B.x·x4m C.(x3m+1)m D.x4m+x
本课始终以学生的发展为主线,引导学生发现问题,分析问题,得出结论,应用结论。 同底数幂的乘法法则是将高一级运算转化为低一级运算,体现了数学“化归”思想.教学中从特殊到一般地推导性质,又从一般到特殊地运用性质,使学生在学习知识的过程中体味数学方法和数学精神,提高了学生的数学素质和数学能力,真正落实了新课程标准的要求。
情境导入法:运用人们关心的环保问题导入同底数幂乘法,吸引了学生的注意力。
提问复习法:本课涉及许多以前学过的知识点,在教学过程中适当提问,帮助学生回忆知识,进入主题。
探究法:引导学生自主探究,发现问题,总结归纳,得出结论,增加学生的印象,培养学生的能力。
游戏法:创设小型游戏,激励学生思考问题,锻炼学生的竞争意识,随着练习的处理,学生运用知识的能力得到提高。
3、应用新知识,深化拓展。
例1:计算
(1) 10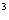 ×10
×10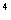 (2) a · a
(2) a · a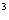 (3)a · a
(3)a · a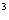 · a
· a


讲解三个例题,让学生了解公式的初步应用,同时也是对公式的推广,针对(3),当三个或三个以上同底数幂相乘时也具有这一性质吗?。通过学生讨论,分析,归纳,从而得出三个或多个同底数幂相乘时也具有这一性质。 a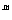 ·a
·a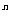 ·a
·a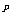 = a
= a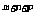
|
|
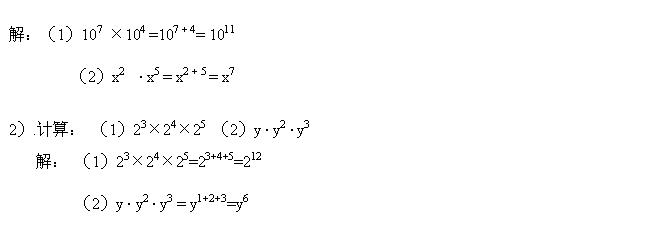 4、巩固练习,形成能力。
4、巩固练习,形成能力。

|
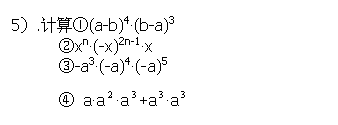



在处理练习的时候,我将学生分成四组,以游戏的形式让学生抢答积分。通过练习,前面的两个知识点得到了巩固。
5,归纳总结,布置作业。
引导学生对本课所学内容进行梳理,发现不足,及时辅导,确保学生掌握所学知识。
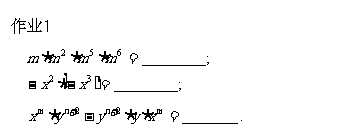

作业2根据乘方的意义及同底数幂的乘法填空:
(1)
(2 )
)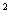 = 2
= 2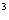 × 2
× 2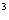 =2(
)
=2(
)
(2)
(a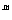 )
)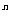 = a(
) (m、n为正整数)
= a(
) (m、n为正整数)
根据本课在教材中地位,作业的布置分成两部分,一部分是巩固,一部分是启发学生思考后面的知识点。
2、发现规律,得出结论。
简单的复习学生已经回忆起乘方的意义,这时让学生进一步了解同底数幂乘法的意义,由特殊到一般,分层推进,让学生发现规律,
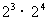
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
=2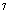 (乘方的意义)
(乘方的意义)
5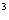 ×5
×5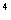
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=5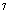
a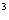 · a
· a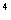
=(a · a · a) (a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
=a7 (乘方的意义)
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
a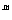 · a
· a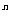 =
=
猜想: a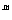 · a
· a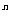 =
(当m、n都是正整数)
=
(当m、n都是正整数)
从而导出同底数 幂乘法公式(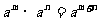 ).此结论正好解决了前面提出的问题。学生很容易得出
).此结论正好解决了前面提出的问题。学生很容易得出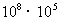 =
=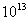 .
.
3、a · a · · · · · · a = a( )
2、a·a·a·a·a = a( )
1、2×2 ×2=2( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com