4．如图3所示，△ABC是△DEF经过平移得到的，若AD=4cm，则BE=_____，CF=________；若M为AB中点，N为DE中点，则MN=_______．

3．如图2所示，∠DEF是∠ABC经过平移得到的，∠ABC=33°，则∠DEF=_____．

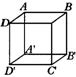
2．如图1所示，四边形ABCD沿着AA′方向，平移到四边形A′B′C′D′，则点A的对应点是点______；点B的对应点是点________；线段AB的对应线段是线段_______；∠DAB的对应角是________；四边形ADD′A′沿着D′C′平移到四边形______；四边形ABB′A′沿着_______方向，平移到______．

　　　　　　 (1)　　　　　　　 (2)　　　　　　　　　　　 (3)

1．平移是由____________所决定．

2．选用课时作业设计．

第一课时作业设计

1．课本P71习题15．1第1，2题．

　　 课本P67练习第2题．

2．出示投影6　 课本P67图15．1．4

　　 学生观察图形．

　　 教师问：△ABC沿BB′方向平移到△A′B′C′，你知道线段CA的中点M平移到什么地方去吗？BC上的点N平移到什么地方去了吗？

　　 在同学交流的基础上，老师可以加以小结：

　　 (1)平移定义：在平面内，将一个图形沿着某个方向移动一定距离，这样的图形运动称为平移．

　　 (2)平移不改变图形的形状和大小．“将一个图形沿着某个方向移动一定的距离”这表明“图形上每个点”都沿着同一方向移动了相同的距离．

1．出示投影5　 传送带上的电视机

　　 教师问：

　　 (1)传送带上的电视机作什么运动？

　　 (2)传送带上的电视机的形状、大小在运动前后是否发生变化？

　　 (3)传送带上的电视机的某一按键向前移动了80cm，那么电视机的其他部位向什么方向移动，移动了多少距离？

　　 学生交流思想．

4．出示投影4　 课本P67图15．1．3

　　 学生观察图形．

　　 教师问：我们学过画平行线用直尺和三角板如何操作，这种运动形式是什么？这里的AB与A′B′位置关系怎样？

　　 学生在互相交流后形成共识：

　　 (1)△ABC沿着直尺PQ平移到△A′B′C′，这里的A与A′，B与B′，C与C′是对应点，线段AB与A′B′，AC与A′C′，BC与B′C′是对应线段，∠A与∠A′，∠ABC与∠A′B′C′，∠BAC与∠B′A′C′是对应角，发现对应线段是平行的，也可能在同一条直线上，如BC和B′C′，画AB的平行线A′B′就是平移的一个例证．

　　 (2)△ABC的平移方向，就是点B到B′的方向；也可以说由A到A′的方向；也可以说由C到C′的方向，平移的距离就是线段BB′的长度；也可以说是线段AA′或CC′的长度．