1．两个学生一个小组，一人抛掷，一人记录。

　　 每个小组抛掷40次，记录出现钉尖触地的频数。

　　 教师负责把各小组的结果登录在黑板上。

　　 上一节课，通过一系列的实验和观察，我们已经知道：实验是估计机会大小的一种方法。我们可以通过实验，观察某事件出现的频率，当频率值逐渐稳定时，这个值就可以作为我们对该事件发生机会的估计。

　　 实际上，在前面的问题中，即使不做实验，也可以设法预先推测出事件发生的机会，为什么还要花大量时间去进行实验呢?

　　 下面让我们看另一类问题：

一枚图钉被抛起后钉尖触地的机会有多大?

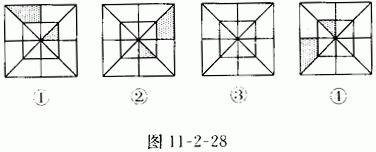
14．(4分)分析图11-2-28①②④中阴影部分的分布规律。按此规律在图③中画出其中的阴影部分．

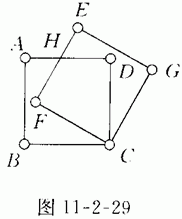
　　 (2004·上海)如图11-2-29，边长为3的正方形ABCD绕点C按顺时针方向旋30°后得到正方形EFCG,EF交AD于点H,那么DH的长为　　　　　　．

13．(4分)设计一个旋转对称图案，使其旋转60°后能与自身重合．

[自主探究题]

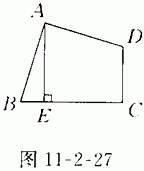
12．(6分)如图11-2-27，四边形ABCD中， ∠BAD＝∠BCD=90°,AB＝AD，AE⊥BC，垂足为E,若四边形ABCD的面积是16，求AE的长．

[开放题]

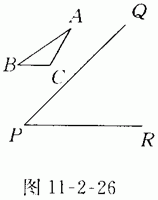
11．(6分)如图11-2-26，在纸上画△ABC和过点P的两条直线PQ、PR,且∠RPQ=45°,先画出△ABC关于PQ对称的三角形A'B'C'，再画出△A'B'C'关于PR对称的 △A"B"C"．请回答△ABC与△A"B"C"的关系是什么?∠APA"是多少度?

新课标拓展训练(共计14分)

[创新实践题]

10．(5分)如图11-2-25，将半圆绕半圆上一点P顺时针旋转90°．

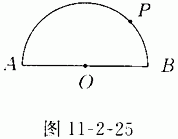
[应用题]

[创新情景题]

9．(4分)如图11-2-24, 这是我国出土的古代陶器的图案，问图形绕中心旋转多少度后能与自身重合．

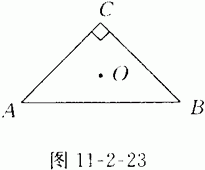
8．(3分)如图11-2-23，△ABC是等腰直角三角形，∠C＝90°,AC＝BC，点O是三条中线的交点，△ABC以点O为旋转中心，旋转多少度后能与原来的图形重合?

[学科间综合]

7．(3分)下列图形是旋转对称图形的有(　　 )

　　　 　①等腰梯形　 ②五角星　 ③平行四边形　 ④等边三角形　 ⑤等腰三角形

　　　 　A.2个　　　　　　 B. 3个　　　　　　 　C. 4个　　　　　　　　D．5个