
15.2乘法公式之完全平方公式
教学目标:
完全平方公式的推导及其应用.完全平方公式的几何解释.视学生对算理的理解,有意识地培养学生的思维条理性和表达能力.
教学重点:
完全平方公式的推导过程、结构特点、几何解释,灵活应用
教学过程设计:
|
设计意图 |
第一课时 (一)提出问题,学生自学 1.问题:根据乘方的定义,我们知道:a2=a·a,那么(a+b)2 应该写成什么样的形式呢?(a+b)2的运算结果有什么规律?计算下列各式,你能发现什么规律? (1)(p+1)2=(p+1)(p+1)=_______; (m+2)2=_______; (2)(p-1)2=(p-1)(p-1)=________; (m-2)2=_______; 2.学生探究[1] 3.得到结果:(1)(p+1)2=(p+1)(p+1)=p2+2p+1 (m+2)2=(m+2)(m+2)= m2+4m+4 (2)(p-1)2=(p-1)(p-1)= p2-2p+1 (m-2)2=(m-2)(m-2=m2-4m+4 4.分析推广:结果中有两个数的平方和,而2p=2·p·1,4m=2·m·2,恰好是两个数乘积的二倍。(1)(2)之间只差一个符号。 推广:计算(a+b)2=_____ ___ (a-b)2=_____ ___ [2] (二)得到公式,分析公式 1.结论: (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 即: 两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍. 2.几何分析:[3] 
 图(1),可以看出大正方形的边长是a+b,它是由两个小正方形和两个矩形组成,所以大正方形的面积等于这四个图形的面积之和.[4] (三)运用公式 |
|
设计意图 |
1. 直接运用[1] 例:应用完全平方公式计算: (1)(4m+n)2 (2)(y-  )2 )2 (3)(-a-b)2 (4)(b-a)2 练习:P155 练习1,2 2. 简便计算[2] 例:运用完全平方公式计算: (1)1022 (2)992 练习:计算: 50.012 49.92 附加练习: 计算:    )2= )2=  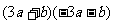  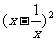 在下列多项式中,哪些是由完全平方公式得来的?   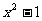 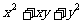  (四)小结: 完全平方公式的结构特征. 公式的左边是一个二项式的完全平方;右边是三项,其中有两项是左边二项式中每一项的平方.而另一项是左边二项式中两项乘积的2倍. |
|
|
|
|
作业 |
课本P156复习巩固2 |
|
设计意图 |
第二课时:(添括号法则在公式里的运用) (一) 回顾完全平方公式 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (二) 提出问题,解决问题 1. 在运用公式的时候,有些时候我们需要把一个多项式看作一个整体,把另外一个多项式看作另外一个整体。例如:  和 和 ,这就需要在式子里添加括号。那么如何加括号呢?它有什么法则呢?它与去括号有何关系呢?[1] ,这就需要在式子里添加括号。那么如何加括号呢?它有什么法则呢?它与去括号有何关系呢?[1]2. 解决问题: 在去括号时: 
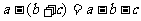 反过来,就得到了添括号法则: 
 3. 理解法则:如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号. 也是:遇“加”不变,遇“减”都变. 4. 运用法则: [2] (1)a+b-c=a+( ) (2)a-b+c=a-( ) (3)a-b-c=a-( ) (4)a+b+c=a-( ) 2.判断下列运算是否正确. (1)2a-b-  =2a-(b- =2a-(b- ) (2)m-3n+2a-b=m+(3n+2a-b) ) (2)m-3n+2a-b=m+(3n+2a-b)(3)2x-3y+2=-(2x+3y-2) (4)a-2b-4c+5=(a-2b)-(4c+5) 5. 总结: 添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,所以我们可以用去括号法则验证所添括号后的代数式是否正确. (三) 在公式里运用法则[3] 例:计算:(1)(x+2y-3)(x-2y+3) (2)(a+b+c)2 (3)(x+3)2-x2 (4)(x+5)2-(x-2)(x-3) 练习:P156练习1,2 计算: 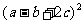  、 、(四) 两公式的综合运用 例:如果 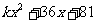 是一个完全平方公式,则 是一个完全平方公式,则 的值是多少?[4] 的值是多少?[4]练习:如果  是一个完全平方公式,则 是一个完全平方公式,则 的值是多少? 的值是多少?例:如果  ,那么 ,那么 的结果是多少?[5] 的结果是多少?[5]练习:已知   ,求 ,求 和 和  的值 的值 |
|
设计意图 |
已知 ,求 ,求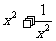 和 和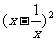 的值 的值已知 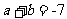  ,求 ,求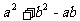 和 和  的值 的值附加:证明  能被4整除 能被4整除(五)小结:利用添括号法则可以将整式变形,从而灵活利用乘法公式进行计算,灵活运用公式进行运算 |
|
|
|
|
作业 |
课本P156综合运用3、4 |
15.2乘法法公式之平方差公式
教学目标:
经历探索平方差公式的过程.会推导平方差公式,并能运用公式进行简单的运算,培养学生观察、归纳、概括的能力.
教学重点:平方差公式的推导和应用.理解平方差公式的结构特征,灵活应用平方差公式.
教学过程设计:
|
设计意图 |
(一) 学生动手,得到公式 1. 计算下列多项式的积. (1)(x+1)(x-1) (2)(m+2)(m-2) (3)(2x+1)(2x-1) (4)(x+5y)(x-5y) 2.提出问题: 观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律? 3.特点: 等号的一边:两个数的和与差的积,等号的另一边:是这两个数的平方差 4.再试一试: [学生自己出相似的题目加以验证] 5.得到结论 (a+b)(a-b)=a2-ab+ab-b2=a2-b2. 即 (a+b)(a-b)=a2-b2 [1] (二) 熟悉公式 1.下列哪些多项式相乘可以用平方差公式? 
 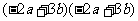
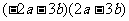  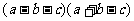 1. 认清公式:在等号左边的两个括号内分别没有符号变化的集团是a,变号的是b (三) 运用公式 1. 直接运用 例:(1)(3x+2)(3x-2)(2)(b+2a)(2a-b)(3)(-x+2y)(-x-2y) 2. 简便计算 例:(1)102×98[3] (2)(y+2)(y-2)-(y-1)(y+5) 3. 练习: P153 练习1,2     100.5×99.5 99×101×10001 |
|
[1]其中a、b表示任意数,也可以表示任意的单项式、多项式. |
|
设计意图 |
(四)公式的几何关系 附加题: 1. 证明:两个连续奇数的积加上1一定是一个偶数的平方 2. 求证:  一定是24的倍数 一定是24的倍数(四) 小结: 1、 记住平方差公式 2、 平方差公式的直接利用及简便应用 |
|
[1]体现数形结合的思想 |
|
|
作业 |
课本P156复习巩固1 |
|
板书设计 |
§15.2.1 平方差公式 一.探究、归纳规律──平方差公式 文字语言:两数和与这两数差的积,等于它们的平方差 符号语言:(a+b)(a-b)=a2-b2 二.1.用简便方法计算 2.计算: 三.应用、升华: |
22.观察下面各式:
12+(1×2)2+22=(1×2+1)2
22+(2×2)2+32=(2×3+1)2
32+(3×4)2+42=(3×4+1)2
……
(1)写出第2005个式子;
(2)写出第n个式子,并说明你的结论.

21.若f(x)=2x-1(如f(-2)=2×(-2)-1,f(3)=2×3-1),求 的值.
的值.
20.化简(x+y)+(2x+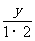 )+(3x+
)+(3x+ )+…+(9x+
)+…+(9x+ ),并求当x=2,y=9时的值.
),并求当x=2,y=9时的值.
19.已知(a+b)2=60,(a-b)2=80,求a2+b2及ab的值.
18.(2003·郑州)如果(2a+2b+1)(2a+2b-1)=63,求a+b的值.
17.已知a=1990x+1989,b=1990x+1990,c=1990x+1991,求a2+b2+c2-ab-ac-bc的值.
16.解不等式(1-3x)2+(2x-1)2>13(x-1)(x+1).
15.已知(t+58)2=654481,求(t+84)(t+68)的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com