
3、 算一算
例一 教科书第173页例4
例二 小民的步长为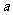 米,他量得家里的卧室长15步,宽14步,这间卧室的面积有多少平方米?
米,他量得家里的卧室长15步,宽14步,这间卧室的面积有多少平方米?
解:
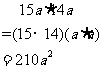
答:这间卧室的面积为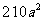 平方米。
平方米。
2、 试一试:
类似地,请你试着计算: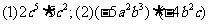
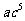 和
和 ,
, 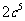 和
和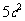 ,
, 和
和 都是单项式,通过刚才的尝试,谁能告诉大家怎样进行单项式乘法?
都是单项式,通过刚才的尝试,谁能告诉大家怎样进行单项式乘法?
学生小结:单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
1、问题:如果将上式中的数字改为字母,即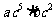 ,你会算吗?
,你会算吗?
学生独立思考。
学生分析:跟刚才的解决过程类似,可以将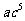 和
和 分别看成
分别看成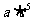 和
和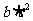 ,再利用乘法交换律和结合律。
,再利用乘法交换律和结合律。
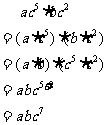
2、练一练
口答:
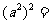
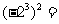

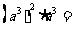
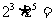
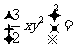
创设情景引入新课
问题 光的速度约为
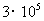 千米/秒,太阳光照射到地球上需要的时间大约是
千米/秒,太阳光照射到地球上需要的时间大约是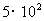 秒,你知道地球与太阳的距离约是多少千米吗?
秒,你知道地球与太阳的距离约是多少千米吗?
地球与太阳的距离约为 千米。
千米。
问题是 等于多少呢?
等于多少呢?
学生提出用乘法交换律和结合律可以解决:
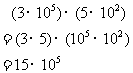
在此处再问学生更加规范的书写是什么?
应该是地球与太阳的距离约为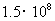 千米。
千米。
请学生回顾,我们是如何解决问题的。
探究新知:
1、知识回顾:
回忆幂的运算性质:
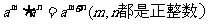
即同底数幂相乘,底数不变,指数相加。
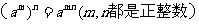
即幂的乘方,底数不变,指数相乘。
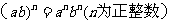
即积的乘方,等于把积的每一个因式分别成方,再把所得的幂相乘。
2、 让学生主动参与到探索过程中去,逐步形成独立思考、主动探索的习惯,培养思维的批判性、严密性和初步解决问题的愿望与能力。
教学重点与难点:
重点:单项式与单项式、单项式与多项式相乘的法则。
难点:单项式与多项式相乘去括号法则的应用。
教学设计:
复习引新
1、 探索并了解单项式与单项式、单项式与多项式相乘的法则,并运用它们进行运算。
15.2.4整式的乘法(3)
教学目标:
2、适时的辨明和恰当的拓展、延伸,效果特佳,并能增强课堂的兴趣,发展学生的思维能力。
布置作业:课本后附作业题
[设计思想]
1、本课时在已有的同底数幂相乘法则和幂的乘方法则,以及乘方的意义的基础上,通过合作交流,探索归纳得出积的乘方法则,正是从建构主义观点出发而一环一环设计而成的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com