
例1 如课本P74图15.2.6,△ABC是等边三角形,D为BC一点,△ABD经过旋转到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
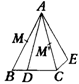
分析:(1)△ABD是绕着点A按逆时针方向旋转到△ACE的位置,所以点A应是它的旋转中心.
(2)由于AB与AC是△ABD与△ACE的对应边,即AB绕着点A旋转到AC的位置,所以它的旋转角为∠BAC=60°.
(3)根据旋转原理,△ABD上各点都是绕着点A旋转到△ACE的位置,所以AB的中点M也应转到AB的对应线段AC的中点M′处.
解:(1)旋转中心是A.
(2)旋转了60°.
(3)点M转到AC的中点M′处.
例2 如课本P74图15.2.7所示,(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段位置有何关系?
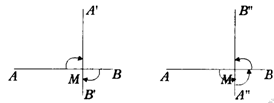
(2)将线段AB绕着点M,逆时针方向旋转90°呢?
分析:(1)把线段AB绕着M按顺时针方向旋转90°,即到A′B′位置,由于AB交A′B′于M,成90°角,所以AB与A′B′互相垂直.
(2)把线段AB绕着M按逆时针方向旋转90°,即到A″B″位置,由于A″B″交AB于M成90°角,所以A″B″与AB互相垂直.
解:(1)A′B′与AB互相垂直.
(2)A″B″与AB互相垂直.
3.出示投影5 课本P73图15.2.5
学生在观察对照中,教师提出问题:
△ABC和△A′B′C′的顶点、边、角是如何对应的呢?
(1)点A与点A′,点B与点B′,点C与点C′是对应点.
(2)线段AB与线段A′B′,线段BC与线段B′C′,线段AC与线段A′C′是对应线段(即对应边).
(3)∠A与∠A′,∠B与∠B′,∠C与∠C′是对应角.
2.出示投影4 课本P73图15.2.5
同学们在交流中形成共识后,教师可以让学生回答如下问题:
(1)B点旋转到哪一点?(点B′)
(2)C点旋转到哪一点?(点C′)
(3)∠BAC旋转到哪里?(∠B′AC′)
(4)线段AB旋转到哪里?(线段AB′)
(5)线段AC旋转到哪里?(线段AC′)
(6)线段BC旋转到哪里?(线段B′C′)
(7)∠B旋转到哪里?(∠B′)
(8)∠C旋转到哪里?(∠C′)
(9)它的旋转中心是什么?(点A)
(10)它的旋转的角度是多少?(45°)
这里要给学生指出:在旋转的过程中,(1)点B与点B′,点C和点C′是对应点;(2)线段AB与线段AB′,线段AC与AC′,线段BC与线段B′C′是对应线段;(3)∠BAC和∠B′AC′,∠B与B′,∠C与∠C′是对应角.
想一想:△ABC的边AB的中点D的对应点在哪里?
根据旋转的原理:图形上每一个点都绕着旋转中心,按同一方向,旋转同一角度而得到的,所以AB的中点D的对应点也应在它的对应线段AB′的中点位置.
做一做:如果△ABC的外面一点O作为旋转中心,把△ABC绕着点O按逆时针方向旋转60°,将△ABC旋转到△A′B′C′位置,你会做吗?在学生动手操作下,不会的同学也可以互相交流.
1.做一做:大家把准备好的透明纸拿出来.(上节已布置)
按老师要求完成以下内容:
(1)任意画一个△ABC.
(2)把透明纸覆盖在△ABC上,并在透明纸上画出一个与△ABC重合的三角形.
(3)把一枚图钉在点A处固定.
(4)将透明纸绕着图钉(即点A)转动45°,透明纸上的三角形就旋转了新的位置,标上A′、B′、C′.
我们可以认为△ABC绕着A点旋转45°后到△AB′C′.
同学们考虑一下,可以互相交流,在这样的旋转中,你发现了什么?
3.出示投影3 课本P72图15.2.3
学生观察图形.
教师提出问题:
(1)单摆上小球的转动由位置P转到P′,它是绕着哪一点?沿着什么方向?转动了多少角度?
(2)单摆上小球转到P与P′中间时,它绕着的点、沿着的方向有没有变化?转动的角度有没有变化?
学生在讨论中形成共识后,老师还应在加深旋转概念上加以巩固和深化.
2.出示投影2 课本P72图15.2.2
学生观察上面两个画面.
老师提出:这是法国数学家庞加莱(1854-1912)创设的几何模型,它们与投影1中的三种图形,有何共同点?
同学们在思考、交流的过程中形成共识后,教师板书旋转的定义:平面内将一个图形绕着一个定点,沿着某个方向转动一个角度,这样的图形运动,称为旋转,这个定点叫做旋转中心,转动的角称为旋转角,旋转不改变图形的形状和大小.
这里还应强调三点:
(1)旋转的过程中,旋转中心始终保持不动.
(2)旋转的过程中,旋转的方向是相同的.
(3)旋转的过程静止时,图形上每一点的旋转角是一样的.
由此得出:图形的旋转由旋转中心和旋转的角度所决定.
1.出示投影1 课本P72图15.2.1
学生观察图形,并分析以下问题.
教师问:
(1)上面情景中,哪些零部件作转动?
(2)在这些转动中有哪些共同特征?
(3)钟上的秒针在不停的转动中,其形状、大小、位置是否发生改变?大风车在转动中其形状、大小、位置是否发生改变?彩票大转盘在转动的过程中其形状、大小、位置是否发生变化?
学生交流问题(2)形成共识.
老师指出:这就是今天我们所研究的课题“图形的旋转”(板书).
例1 在方格纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.
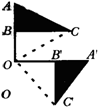
分析:在方格纸上要作出“小旗子”绕点O按顺时针方向旋转90°后的图案,只要按照要求找出A、B、C的对应点即可.
解:(1)作OA′⊥OA,取OA′=OA,OB′=OB;
(2)连OC;
(3)作OC′⊥OC,取OC′=OC;
(4)连A′C′、B′C′.
即可求出如图 “小旗子”按要求旋转后的图案.
点评:这种画图的依据完全根据旋转的基本性质进行作图的.
例2 已知等边△ABC,绕着点B按照逆时针方向旋转120°后的三角形,如图所示.
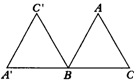
分析:要作等边△ABC绕着B点旋转120°后的三角形,就要按照要求找到满足条件的A的对应点和C的对应点.
由于A要按逆时针方向旋转120°.
所以要在△ABC的左边作∠A′BA=120°.
由于旋转中心到对应点的距离相等.
所以取A′B=AB,即点A′是点A的对应点.
由于△ABC是等边三角形,所以∠ABC=60°.
因此A′、B、C在一直线上.
同样也可以找到C的对应点C′.
连A′C′、BC′,即可获得满足条件的三角形.
解法一:(1)延长CB到A′,使A′B=AB.
(2)作∠A′BA的平分线BC′,取BC′=BC.
(3)连A′C′.
则△A′B′C′是等边△ABC绕着B点旋转120°后所得的三角形.
解法二:(1)延长CB到A′,使A′B=AB.
(2)分别以A′,B为圆心,以A′B长为半径,在直线A′C上侧得到交点C′.
(3)连A′C′,C′B.
则△A′BC′就是满足条件的三角形.
出示投影1 课本P73图15.2.4
学生认真观察图中线段之间和角之间的关系,在教师的帮助下,学生完善数学语言的表述,并形成共识后.
教师板书:旋转的基本性质.
经过旋转,图形上的每一个点都绕着旋转中心,沿着相同的方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
我们可以看到上图中,线段OA,OB都是绕着点O旋转45°角到对应线段OA′与OB′,根据观察的结果OA=OA′,OB=OB′,AB=AB′,∠AOA′=∠BOB′=45°,同时∠AOB=∠A′O′B′,∠A=∠A′,∠B=∠B′.
出示投影2 课本P73图15.2.5
学生观察上图,探索图中线段之间与角之间的关系,根据旋转的基本性质填空.
在课本图15.2.5中,旋转中心是点O,点A、B、C都是绕着点O旋转60°角到对应点A′、B′、C′,则
OA=_______,OB=________,OC=_______,
AB=_______,BC=________,CA=_______,
∠CAB=________,∠ABC=_______,∠BCA=________.
∠AOA′=_______=_______=______=60°
△ABC和△A′B′C′的形状、大小有何变化?_______.
综上所述:图形旋转的特征是图形中每一个点都绕着旋转中心旋转了同样大小的角度.
对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.
3、在探索过程中,利用运算律将问题转化,使学生获得成就感,培养学习数学的兴趣。
[教学重点、难点]
重点是单项式与单项式和单项式与多项式相乘的运算法则及其应用。
难点是如何灵活进行单项式的乘法运算。
[教学准备]
展示课件。
[教学过程]
|
教学过程 |
设计说明 |
|
一、回顾与思考 简单回顾新学的有关幂的运算性质,鼓励学生参与回顾。 二、创设情景,引出课题。 展示:天安门广场 展示:一位旅行者用步长测量天安门广场的面积:他从南到北,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积。 (1)如果用字母a表示该旅行者的步长,你能用含a的代数式表示广场的面积吗? (1100a)×(625a) (2)假设这位旅行者的步长为0.8m,那么广场的面积大约是多少m2? (1100×0.8)×(625×0.8)=440000m2 (3)通过解决上述问题,你认为两个单项式相乘应怎样运算?运算依据是什么? 教师引导,学生参与,从具体实行(1100×0.8)×(625×0.8)=1100×625×0.82开始运用乘法交换律、乘法结合律、同底数幂的运算性质能得出: (1100a)×(625a)=(1100×625)×(a×a)=(1100×625)a2 二、诱向深入,构建模型 类似的3x2y·2x3y2,(abc)·(a2c)怎么办呢? 学生小组交流,合作学习,老师进行引导总结: (1)系数与系数相乘 (2)同底数幂与同底数幂相乘 (3)其余字母及其指数不变作为积的因式 师:以上各题正是单项式与单项式相乘,总结得到的三点正是单项式与单项式相乘法则。 三、展示应用,评价自我。 1、做一做。(学生到黑板前演示,之后师生共同评定) (1)3b3·5/6b2 (2)(-6ay3)(-a2) (3)(-3x)3(5x2y) (4)(2×104)(6×103)·107 注意点:(1)任何一个因式都不可丢掉 (2)结果仍是单项式 (3)要注意运算顺序 2、练一练 课本P121 1、2 四、合作学习,再觅新知 一幅电脑画的尺寸如图5-3(详见课本P170) (1)请用两种不同的方法表示画面的面积; 方法一:a(a-2m) 方法二:ab-am-am=ab-2am (2)这两种不同方法表示的面积应当相等,你所用运算律解释它们相等吗? (体会分配律及其转化) (3)通过上面讨论,你能总结出单项式与多项式相乘的运算规律吗? 学生小组讨论,合作学习,逐步从a(b-2m)=ab-2am中提炼出单项式与多项式相乘的法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。(注意:项是包括符号的) 五、应用新知,体验成功。 1、试一试(教师与学生共同完成) (1)2a2b(1/2ab-3ab2) (2)(1/3x-3/4xy)(-12y) 2、练一练 课本P122课内练习3。 六、归纳小结,充实结构。 1、单项式与单项式相乘法则 2、单项式与多项式相乘法则 3、法则是由哪些运算律转化而来的? 七、知识留恋,课后韵味。 布置作业:1、课后作业题 2、课本P123设计题 |
温故而知新 由实际中的具体问题引出数学问题,进一步加强学生对数学的兴趣。 从特殊到一般,从具体到抽象。 运算律的转化使用 进行更深入的探讨,学会总结运算中的规律。 展示自我,有错纠之,无则加勉。 通过实际情景和合作学习的方式,使学生更易体会事物之间的联系,加深印象。 及时巩固,及时反馈,更有利于知识的掌握。 在教师引导下,学生自主进行归纳,能够使新学的知识及时地纳入学生的认知结构。 设计题能培养学生的综合实践能力,是一个好题材。 |
[设计说明]:
本节课通过创设情景和合作学习引入新知识,使得知识的构建比较自然,通过设计问题,使学生体会到相关运算律的转化,并体验从特殊到一般,从具体到抽象,抽象又服务于具体的认知规律。同时,通过两段论式的设计,分解新知识的难度,使得学生能分步掌握知识。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com