
连PB、PB′、PB″,而得PB=PB′=PB″,同样PC=PC′=PC″,PA=PA′=PA″,∠BPM=∠B′PM,∠B″PM′=∠PB′M′,即∠BPB″=2∠P,…….
根据旋转的基本特征,可以得到△A″B″C″是△ABC绕着P点按逆时针方向旋转2∠P角度后得到的.
课本P78练习第1,2,3,4题.
4.连A″B″、B″C″、A″C″,则△A″B″C″是△A′B′C′关于PR的对称三角形.
请大家观察一下△ABC和△A″B″C″有何关系.
经过交流、探索、评判△A′B′C′是△ABC绕着P点旋转2∠P后得到的.
3.作A′、B′、C′关于PR的对称点A″、B″、C″;
2.连A′B′、B′C′、A′C′,则△A′B′C′是△ABC关于PQ的对称三角形;
做一做:在纸上画△ABC和过点P的两直线PQ、PR,画出△ABC关于PQ的对称△A′B′C′,再画出△A′B′C′关于PR对称的△A″B″C″,如图所示.
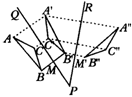
请同学们根据要求作出△A′B′C和△A″B″C″.
学生画图后,交流和评判.
教师把作图过程进行阐述,或者请层度中等的同学把画图过程说明,教师根据学生的描述在黑板上操作.
1.作A、B、C关于PQ的对称点A′、B′、C′;
下图是否为旋转对称图形?如果是,请找出它的旋转中心,旋转多少度后能与自身重合.
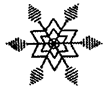
分析:利用半透明纸和图钉操作,可以发现它的确是旋转对称图形,它外围的六个点与中心的距离相等,并且可以看成以中心为圆心,以外围一个点到中心的距离长为半径的圆的六等分点.
解:它的旋转中心是它的中心,旋转60°后能与自身重合,或且旋转120°后能与自身重合,或且旋转180°后能与自身重合,或且旋转240°后能与自身重合,所以它是旋转对称图形.
2.出示投影2 课本P76图15.2.9
同学们能不能也用刚才用透明纸的办法,检验这图形是否也是旋转对称图形呢?
教师提问:
(1)该图形绕着哪一点旋转?旋转多少度后能与自身重合?
(2)它与投影1的两图有何共同特征?
在同学解答、交流、评判的过程中,教师小结:课本图15.2.9绕着圆心旋转60°后,能与自身重合,而且绕圆心旋转120°或180°后都能和自身重合.
它与投影1的两图也是通过绕中心旋转一定角度后与自身完全重合.
这种图形即绕着一个定点,旋转一定角度后能与自身重合的图形称为旋转对称图形.
这也是检验一个图形是否为旋转对称图形的依据.
自古以来,对称形式被认为是和谐美丽、并且真实的,不论是在自然界中还是在建筑里,甚至最普通的日常生活用品中,对称的形式随处可见.请同学们例举出现实生活中旋转对称图形的例子,进行交流.
1.出示投影1 课本P76图15.2.8
学生观察图形.
老师用一张半透明纸,覆盖在图15.2.8上,并在薄纸上画这两个图形,使它们与图15.2.8所示的图形重合,然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转多少度后(小于周角)薄纸上的图形能与原图形再一次重合.
由上述操作可知:电扇的叶片转动120°后能与自身重合,螺旋桨转动180°后能与自身重合.
这让我们想起轴对称来,这些图形如果沿着某条直线对折、对折的两部分是完全重合的,这样的图形称为轴对称图形,这里的轴对称图形指的是一个图形,用的是对折的办法,使对折的两部分是完全重合的,可今天我们也是对一个图形来说,但它不是采用对折使两部分重合,而是通过绕着一个点旋转一定角度后,旋转后的图形与原图形重合,这也是一种对称吗?回答应该是肯定的,它确实也是一种对称,称为旋转对称图形,这就是今天我们所要研究的课题:旋转对称图形(板书)
例1 在方格纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.
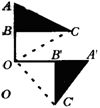
分析:在方格纸上要作出“小旗子”绕点O按顺时针方向旋转90°后的图案,只要按照要求找出A、B、C的对应点即可.
解:(1)作OA′⊥OA,取OA′=OA,OB′=OB;
(2)连OC;
(3)作OC′⊥OC,取OC′=OC;
(4)连A′C′、B′C′.
即可求出如图 “小旗子”按要求旋转后的图案.
点评:这种画图的依据完全根据旋转的基本性质进行作图的.
例2 已知等边△ABC,绕着点B按照逆时针方向旋转120°后的三角形,如图所示.
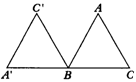
分析:要作等边△ABC绕着B点旋转120°后的三角形,就要按照要求找到满足条件的A的对应点和C的对应点.
由于A要按逆时针方向旋转120°.
所以要在△ABC的左边作∠A′BA=120°.
由于旋转中心到对应点的距离相等.
所以取A′B=AB,即点A′是点A的对应点.
由于△ABC是等边三角形,所以∠ABC=60°.
因此A′、B、C在一直线上.
同样也可以找到C的对应点C′.
连A′C′、BC′,即可获得满足条件的三角形.
解法一:(1)延长CB到A′,使A′B=AB.
(2)作∠A′BA的平分线BC′,取BC′=BC.
(3)连A′C′.
则△A′B′C′是等边△ABC绕着B点旋转120°后所得的三角形.
解法二:(1)延长CB到A′,使A′B=AB.
(2)分别以A′,B为圆心,以A′B长为半径,在直线A′C上侧得到交点C′.
(3)连A′C′,C′B.
则△A′BC′就是满足条件的三角形.
出示投影1 课本P73图15.2.4
学生认真观察图中线段之间和角之间的关系,在教师的帮助下,学生完善数学语言的表述,并形成共识后.
教师板书:旋转的基本性质.
经过旋转,图形上的每一个点都绕着旋转中心,沿着相同的方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
我们可以看到上图中,线段OA,OB都是绕着点O旋转45°角到对应线段OA′与OB′,根据观察的结果OA=OA′,OB=OB′,AB=AB′,∠AOA′=∠BOB′=45°,同时∠AOB=∠A′O′B′,∠A=∠A′,∠B=∠B′.
出示投影2 课本P73图15.2.5
学生观察上图,探索图中线段之间与角之间的关系,根据旋转的基本性质填空.
在课本图15.2.5中,旋转中心是点O,点A、B、C都是绕着点O旋转60°角到对应点A′、B′、C′,则
OA=_______,OB=________,OC=_______,
AB=_______,BC=________,CA=_______,
∠CAB=________,∠ABC=_______,∠BCA=________.
∠AOA′=_______=_______=______=60°
△ABC和△A′B′C′的形状、大小有何变化?_______.
综上所述:图形旋转的特征是图形中每一个点都绕着旋转中心旋转了同样大小的角度.
对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com