15.3.1平方差公式

教学目标

①经历探索平方差公式的过程，进一步发展学生的符号感和推理能力、归纳能力．

②会推导平方差公式并掌握公式的结构特征，能运用公式进行简单的计算．

③了解平方差公式的几何背景，体会数形结合的思想方法．

教学重点与难点

重点：平方差公式的推导及应用．

难点：用公式的结构特征判断题目能否使用公式．

教学准备

卡片及多媒体课件

教学设计

引入

同学们，前面我们刚刚学习了整式的乘法，知道了一般情形下两个多项式相乘的法则．今天我们要继续学习某些特殊情形下的多项式相乘．下面请同学们应用你所学的知识，自己来探究下面的问题：

探究：计算下列多项式的积，你能发现它们的运算形式与结果有什么规律吗?

(1)(x+1)(x-1)=

(2)(m+2)(m-2)=

(3)(2x+1)(2x-1)=

引导学生用自己的语言叙述所发现的规律，允许学生之间互相补充，教师不急于概括．

注：平方差公式是多项式乘法运算中一个重要的公式，它的得出可以直接利用多项式与多项式相乘的运算法则，利用多项式乘法推导乘法公式是从一般到特殊的过程，对今后学习其他乘法公式的推导有一定的指导意义，同时也可培养学生观察、归纳、概括等能力，因此在教学中，首先应让学生思考：你能发现什么?让学生经历观察(每个算式和结果的特点)、比较(不同算式之间的异同)、归纳(可能具有的规律)、提出猜想的过程，学生在发现规律后，还应通过符号运算对规律进行证明．

举例

再举几个这样的运算例子．

注：让学生独立思考，每人在组内举一个例子(可口述或书写)，然后由其中一个小组的代表来汇报．

验证

我们再来计算(a+b)(a-b)=

公式的推导既是对上述特例的概括，更是从特殊到一般的归纳证明，在此应注意向学生渗透数学的思想方法：特例→归纳→猜想→验证→用数学符号表示．

注：这里是对前边进行的运算的讨论，目的是让学生通过观察、归纳，鼓励他们发现这个公式的一些特点，如公式左右边的结构特征，为下一步运用公式进行简单计算打下基础．

概括

平方差公式及其形式特征．

教师可以在前面的基础上继续鼓励学生发现这个公式的一些特点：如公式左、右边的结构，并尝试说明这些特点的原因．

应用

教科书第180页例1运用平方差公式计算：

(1)(3x+2)(3x-2)

(2)(b+2a)(2a-b)

(3)(-x+2y)(-x-2y)

填表：

对本例的前面两个小题可以采用学生独立完成，然后抢答的形式完成；第三小题可采用小组讨论的形式，要求学生在给出表格所提示的解法之后，思考别的解法：提取后一个因式里的负号，将2y看作“a”，将x看作“b”，然后运用平方差公式计算．

注：(1)正确理解公式中字母的广泛含义，是正确运用这一公式的关键．设计本环节，旨在通过将算式中的各项与公式里的a、b进行对照，进一步体会字母a、b的含义，加深对字母含义广泛性的理解：即它们既可以是数，也可以是含字母的整式．

(2)在具体计算时，当有一个二项式两项都负时，往往不易判明a、b，如第三小题，此时可以通过小组合作交流，放手让学生去思考、讨论，有助于学生思维互补、有条理地思考和表达，更有助于学生合作精神的培养．

(3)例1第(3)小题引导学生多角度思考问题，可以加深对公式的理解．

教科书第180页例2计算：

(1)102×98

(2)(y+2)(y-2)-(y-1)(y+5)

此处仍先让学生独立思考，然后自主发言，口述解题思路，允许他们算法的多样化，然后通过比较，优化算法，达到简便计算的目的．

注：(1)运用平方差公式进行数的简便运算的关键是根据数的形式特征，把相乘的两数化成两数和与两数差的乘积形式，教学时可让学生自己寻找相乘两数的形式特征．

(2)第二小题要引导学生注意到一般形式的整式乘法与特殊形式的整式乘法的区别与联系，强调：只有符合公式要求的乘法，才能运用公式简化运算，其余的运算仍按整式乘法法则进行．

巩固

教科书第18l页练习1、2

练习1口答完成；练习2采用大组竞赛的形式进行，其中(1)(4)由两个大组完成，(2)(3)由另两个大组完成．

注：让学生通过巩固练习，达成本节课的基本学习目标，并通过丰富的活动形式，激发学习兴趣，培养竞争意识和集体荣誉感．

解释

你能根据下面的两个图形解释平方差公式吗?

多媒体动画演示图形的变换过程，体会过程中不变的量，并能用代数恒等式表示．

注：(1)重视公式的几何背景，可以帮助学生运用几何直观理解、解决有关代数问题．

(2)此处将教科书的图15.3-1分解为两个图形，是考虑到学生数与形结合的思想方法掌握的不够熟练；利用两个图形可以清楚变化的过程，便于联想代数的形式．

小结

谈一谈：你这一节课有什么收获?

注：这儿采取的是先由每个学生自己小结，然后由小组代表作答，把教师做小结变成了课堂上人人做小结，有助于学生概括能力、抽象能力、表达能力的提高．同时，由于人人都要做小结，促使学生注意力集中，学习主动性加强．

作业

2．选做题：教科书第185页习题15.3第二大题的(2)、(6)；第三大题的(1)、(3)、(4)；第六大题．

1．必做题：教科书第185页习题15.3第二大题的(1)、(3)、(4)、(5)；第三大题的(2)；第四大题．

4、小华看着电视里的舞蹈节目：七个身穿不同民族服装的舞蹈演员正在面对观众进行队列变换，他陷入了沉思：这7个演员面对观众一共会有几种队列变换呢？……为了解决这一问题，他是这样思考和探索的：

①若只有一个演员A，那就只有队列变换A，共1种；

②若有二个演员A、B，那就有队列变换：AB和BA，共2种；

③若有三个演员A、B、C，那就有队列变换：ABC、ACB、BAC、BCA、CAB、CBA，共6种；

④若有四个演员A、B、C、D，那就有队列变换(小华把这四个字母在纸上不停的变换顺序地排列着、写着)……数数看，哇！有24种，变化如此之快呀，五个、六个、七个演员呢？看来不可再强攻，否则就……，还是智取吧……

再应用表格吧，记得书上有这样的例子，老师也曾示范过，它能更加清楚地反映其中的数字规律呢：

……

⑴你知道这7个舞蹈演员面对观众一共会有几种队列变换吗？说说你的理由。

⑵请你先仔细体会小华的解题策略，然后再探索：2²⁰的末位数字是多少？说说你是怎样想的。例如：25的末位数字是5；2043的末位数字是3。

评价十一

3、八年级学生小颖是一个非常喜欢思考问题而又乐于助人的同学，一天邻居家正在读小学的小明，请小颖姐姐帮忙检查作业：

7×9＝ 63　　　　　　　 8×8＝64

11×13＝143　　　　　　 12×12＝144

23×24＝624　　　　　　 25×25＝625

小颖仔细检查后，夸小明聪明仔细，作业全对了！小颖还从这几道题发现了一个规律。你知道小颖发现了什么规律吗？请用字母表示这一规律，并说明它的正确性。

1、　 计算：

① (6a⁵－7a²+36a³)÷3a²　　　　　 ②(－8a⁴b⁵c÷4ab⁵)·(3a³b²)

③ (3x－2)²　　　 　　　　　　　　　④　 (2x－3)(－2x－3

⑤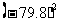　　　　　 (⑥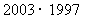

⑦ (2a+1)²－(2a+1)(－1+2a)

_{2、化简求值}

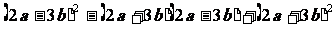
　 其中：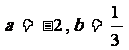

8、一个正方形的边长增加了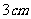，面积相应增加了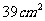，则这个正方形的边长为　　 ㎝

7、月球距离地球大约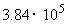千米，一架飞机的速度约为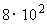千米/时，若乘飞机飞行这么远的距离，大约需要　　　　 　天。

6、我国北宋时期数学家贾宪在他的著作《开方作法本源》中的“开方作法本源图”如下图⑴所示，通过观察你认为图中a＝＿＿＿＿＿＿＿；