1．从乘法与除法互为逆运算的角度．

　　 (1)我们可以想象5.98×10²¹·(　 )=1.90×10²⁴．根据单项式与单项式相乘的运算法则：单项式与单项式相乘，是把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变作为积的因式，可以继续联想：所求单项式的系数乘以5.98等于1.90，所以所求单项式系数为1.90÷5.98≈0.318，所求单项式的幂值部分应包含10²⁴÷10²¹即10³，由此可知5.98×10²¹·(0.318×10³)=1.90×10²⁴．所以(1.90×10²⁴)÷(5.98×10²¹)=0.38×10³．

　　 (2)可以想象2a·(　 )=8a³，根据单项式与单项式相乘的运算法则，可以考虑：8÷2=4，a³÷a=a²　 即2a·(4a²)=8a³．所以8a³÷2a=4a²．

　　 同样的道理可以想象3xy·(　 )=6x³y；

3ab²·(　 )=12a³b²x³，

考虑到6÷3=2，x³÷x=x²，y÷y=1；12÷3=4，a³÷a=a²，b²÷b²=1．

所以得3xy·(2x²)=6x³y；3ab²·(4a²x³)=12a³b²x³．

所以6x³y÷3xy=2x²；12a³b²x³÷3ab²=4a²x³．

2．提倡多样化的算法，培养学生的创新精神与能力．

　　 教学重点

　　 单项式除以单项式的运算法则及其应用．

　　 教学难点

　　 探索单项式与单项式相除的运算法则的过程．

　　 教学方法

　　 自主探索法．

　　 有同底数幂的除法的研究基础，学生可以用已有的知识与数学经验，自主探索得出单项式与单项式相除的运算法则，并能用息的语言有条理地表达及应用．

　　 教具准备

　　 多媒体课件．

　　 教学过程

　　 Ⅰ．提出问题，创设情境

　　 问题：木星的质量约是1．90×10²⁴吨．地球的质量约是5.08×10²¹吨．你知道木星的质量约为地球质量的多少倍吗？

　　 [生]这是除法运算，木星的质量约为地球质量的(1.90×10²⁴)÷(5.98×10²¹)倍．

　　 继续播放：

讨论：

(1)计算(1.90×10²⁴÷(5.98×10²¹)．说说你计算的根据是什么？

　　 (2)你能利用(1)中的方法计算下列各式吗？

8a³÷2a；5x³y÷3xy；12a³b²x³÷3ab²．

(3)你能根据(2)说说单项式除以单项式的运算法则吗？

　　 Ⅱ．导入新课

　　 [师]观察讨论(2)中的三个式子是什么样的运算．

　　 [生]这三个式子都是单项式除以单项式的运算．

　　 [师]前一节我们学过同底数幂的除法运算，同学们思考一下可不可以用自己现有的知识和数学方法解决“讨论”中的问题呢？

　　 (学生以小组为单位进行探索交流，教师可参与到学生的讨论中，对遇到困难的同学及时予以启发和帮助)

　　 讨论结果展示：

　　 可以从两方面考虑：

1．从探索单项式除以单项式的运算法则的过程中，获得成功的体验，积累研究数学问题的经验．

2．理解单项式与单项式相除的算理，发展有条理的思考及表达能力．

1．经历探索单项式除以单项式的运算法则的过程，会进行单项式与单项式的除法运算．

2．单项式除以单项式的运算算理．

1．单项式除以单项式的运算法则及其应用．

3．备选题：下列计算是否正确?如不正确，应怎样改正?

(1)(a-4)(a+4)=a²-4

(2)(2x+5)(2x-5)=2x²-25

(3)(-a-b)(a+b)=a²-b²

(4)(mn-1)(mn+1)=mn²-1

注：作业分层处理有较大的弹性，体现作业的巩固性和发展性原则，尊重学生的个体差异，满足多样化的学习需要，让不同的人在数学上得到不同的发展．

设计思想:

《新课程标准》中明确指出：“数学教学是数学活动的教学，学生是数学学习的主人．教师的职责在于向学生提供从事数学活动的机会，在活动中激发学生的学习潜能，引导学生积极自主探索、合作交流与实践创新．”在教学设计时，我以新课标理念为指导思想，以多媒体教学课件为辅助教学手段，突出对平方差公式的推导和应用．自主探究、举一反三、语言叙述、推导验证、几何解释、应用巩固等活动都是根据学生的认知特点和所学知识的特征，让学生经历数学知识的形成与应用过程，以促进学生有效学习．

在教学活动的组织中始终注意：(1)以问题为活动的核心．在组织活动前，结合学习内容和学生实际，更好地使用教科书(如对平方差公式进行几何解释时，将书中图形一分为二)，创设问题情境．(2)促进学生发展是活动的目的．数学教育要以获取知识为首要目标转变为首先关注人的发展，这是义务教育阶段数学课程的基本理念和基本出发点．因此，本节课我组织活动的目的，不是为了单纯地传授知识，而是注意让学生在参与平方差公式的探究推导、归纳证明、解释应用的过程中促进学生代数推理能力、表达能力、与人合作意识、数学思想方法等各方面的进一步发展．

2．选做题：计算：

(1)x²+(y-x)(y+x)

(2)2008²-2009×2007

(3)(-0.25x-2y)(-0.25x+2y)

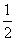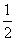(4)(a+b)(a-b)-(3a-2b)(3a+2b)

1．必做题：教科书第184页习题15.3第1题