
5.若(x+y)2=9,(x-y)2=5,则xy=
。
二、计算:
1. 计算:4x(x-1)2+x(2x+5)·(5-2x)
2. 当x=2,y=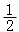 时。
求代数式(x+y)(x-y)+(x-y)2-(x2-3xy)的值。
时。
求代数式(x+y)(x-y)+(x-y)2-(x2-3xy)的值。
2.( -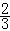 y4)2= -
y4)2= -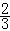 xy4+ 。
3.4a2- +49=( )2。
4.(a+b+c)2=[a+ ]2
=a2+
+
=a2+
+ + + + 。
xy4+ 。
3.4a2- +49=( )2。
4.(a+b+c)2=[a+ ]2
=a2+
+
=a2+
+ + + + 。
布置作业:课本后附作业题
[设计说明]:
本课时通过设计合作学习的图形背景题目来引入新知,理解整式化简的必要性和化简的基本程序,而后通过及时演练反馈来巩固知识,又设计了探究活动,解实际应用题,达到灵活应用知识,自主建构知识之目的。通过本章学习,即掌握了知识,更发展了学生学数学的能力。
今天学到了什么?有何体会?试讲出来与大家交流。
已知a+b=3 ab=1/2 求:
(1)a2+b2 (2)a4+b4
(3)a2+ab+b2
(4)b/a+a/b
2、分析
(1)
|
|
3月份 |
4月份 |
5月份 |
|
甲超市 销售额 |
a |
a(1+x%) |
a(1+x%) x(1+x%) = a(1+x%)2 |
|
乙超市 销售额 |
a |
a(1-x%) |
a(1-x%) x(1-x%) = a(1-x%)2 |
差额为:
a(1+x%)2-a(1-x%)2
2x x2 2x x2 ax
=a(1+--+--)-a(1+--+--)=--(万元)
100 10000 100 10000 25
ax 150×2
(2)当a=150,x=2时,-- = ---= 12(万元)
25 25
1、题目:甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%。
(1)5月份甲超市的销售额比乙超市多多少?
(2)如果a=150,x=2,那么5月份甲超市的销售额比乙超市多多少万元?
2、指导:(学生也可能将所有个位数是5的两位数平方后,直接得到规律,对于这种穷举方法,也应给予鼓励)
(1)、通过计算,探索规律
152=25可写成100×1×(1+1)+25
252=225可写成100×2×(2+1)+25
352=625可写成100×3×(3+1)+25
452=1225可写成100×4×(4+1)+25
……
752=5625可写成
852=7225可写成
(2)从第(1)题的结果、归纳、猜想得
(10n+5)2=
(3)根据上面的归纳、猜想,试计算:
19952=
1、题目:
观察下列各式
52=25
152=225
252=625
352=1225
你能口算末位数是5的两位数的平方吗?请用完全平方公式说明理由。
2、练一练:
(1)化简:
①(x+6)2+(3+x)(3-x)
②3x(x2+3x+8)+(-3x-4)(3x+4)
③(a+b+3)(a+b-3)
(2)当x=-1/3时,求代数式:
(3x+5)2-(3x-5)(3x+5)的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com