在线段.等腰梯形.平行四边形.矩形.菱形.正方形.等边三角形中.既是轴对称图形.又是中心对称图形的图形有 A.3个 B.4个 C.5个 D.6个——青夏教育精英家教网—

0 202708 202716 202722 202726 202732 202734 202738 202744 202746 202752 202758 202762 202764 202768 202774 202776 202782 202786 202788 202792 202794 202798 202800 202802 202803 202804 202806 202807 202808 202810 202812 202816 202818 202822 202824 202828 202834 202836 202842 202846 202848 202852 202858 202864 202866 202872 202876 202878 202884 202888 202894 202902 447090

2.　　　在线段，等腰梯形，平行四边形，矩形，菱形，正方形，等边三角形中，既是轴对称图形，又是中心对称图形的图形有(　 A 　)

A.3个　　　　　 B.4个　　　　　 C.5个　　　　　 D.6个

试题详情

1.　　　下列说法中，不正确的是(　 D　 )

A.轴对称图形的对称轴是对称点连线的垂直平分线

B.中心对称图形的对称中心是对称点连线的中点

C.成轴对称的两个图形中，对应线段相等

D.成中心对称的两个图形中，对应线段平行且相等

试题详情

教师活动

学生活动

设计意图

(一)创设情景，提出问题
请同学欣赏一组轴对称图片.
问题：这一组图片具有什么共同的特点？
可称之为什么图形？
具体分析这一组图片中的一幅----圆，在圆中加一条线段后提出问题：这幅图片是轴对称图形吗？再加一条S线后，仍然问这个问题.
接着提出问题：这幅图片是否能够通过某种图形运动与自身重合呢？

学生进行议论、交流、评判形成共识

一连提出几个问题，使学生产生认知冲突，激发学生解决问题的欲望.在学生学过轴对称图形的基础上，让学生用运动的观点来思考问题，这样易于引起学生的联想，便于新知识的理解和掌握.

(二)探究讨论，发现新知
1．建立中心对称图形的概念
(1)动手操作.
请每位学生拿出事先准备好的一张半透明的薄纸和一张白纸，两张纸上已画有形状、大小相同的图形(如图1)，把两张纸上的图形重合，用一枚图钉在点O处穿过，然后将薄纸绕点O旋转180度.
(从上面的操作可以看到，旋转后的两张纸上的图形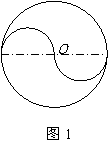

仍然是重合的.)
　
　
　
　
(2)引出概念.
师生共同分析从图形旋转到重合的过程，找出其中的本质特征进行描述，再进行归纳和概括，得到中心对称图形的概念.
把一个图形绕着某一点旋转180°，如果旋转后的图形与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做对称中心.
(3)提出问题.
我们平时见过的几何图形中，有哪些是中心对称图形？并指出它们的对称中心？
(如线段、矩形、平行四边形、圆、…，并指出线段的对称中心是线段的中点；矩形和平行四边形的对称中心是对角线的交点；圆的对称中心是圆心.)
(4)欣赏图片.
展示一组来自生活实际的中心对称图片，让学生观察、欣赏，并关注他们对中心对称图形的感受.
　
2．建立两个图形关于某点对称的概念
(1)　　

研究图片.
继续研究图1

我们知道图1作为一个整体，它是中心对称图形，同时我们也可把它看成是两个图形，将其中的一个图形绕点O旋转180度，会有什么样的结果呢？

学生思考片刻之后、给学生做一个演示，估计学生会很快由观察联想得出两个图形关于某个点对称的概念.

(2)引出概念.

把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么我们就说这两个图形关于这个点对称，这个点叫做对称中心，这两个图形中的对应点，叫做关于中心的对称点.

(引出概念时，注意引导学生正确理解中心对称图形和两个图形成中心对称这两个概念之间的辩证关系，即：把图1看作一个整体，它是中心对称图形，把它看作两个图形时，那么这两个图形关于某点对称.)

3．研究图形性质

问题：两个图形关于某点对称时，对称点和对称中心有什么关系？

先在一个图形上任取三个点，通过旋转找出它们的对称点，连结对称点，然后具体分析其中的一对对称点A、和对称中心O，我们知道点A绕点O旋转180度得到点，所以点A、点和点O三点共线，并且AO=.同理，其他各对对称点也具有这样的特点.借助动画演示，引导学生得出两个图形关于某点对称的性质：

关于中心对称的两个图形，连结对称点的线段都经过对称中心，并且被对称中心平分.

提出问题：如果两个图形的对应点连线都经过某一点，并且被这点平分，那么这两个图形是否关于这一点对称？

得出以下结论：

反过来，如果两个图形的对应点连线都经过某一点，并且被这点平分，那么这两个图形关于这一点对称.

由此我们可以判定两个图形是否关于某一点对称.

观察，动手练习
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
交流、思考、回答
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
思考
　
　
　
　
理解、记忆
　
　
　
　
　
　
　
　
　
　
　
　
思考
　
　
　
　
　
　
　
　
　
　
交流、思考、形成共识
　
　
　
思考、形成共识
　

根据学生的年龄特点，及实验几何的要求，期望让每位学生通过自己动手操作直观得出中心对称图形的概念，并加深对概念的理解.
　
　
　
　
　
　
　
　
　
　
通过以上操作帮助学生加深对中心对称图形概念两个要素(绕某一点旋转180度、旋转后与原图重合)的理解.
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
通过以上操作帮助学生加深对成中心对称的概念的理解.
其表示的是两个图形之间的对称关系
　
　
　
　
　
　
　
注意中心对称图形与成中心对称是相对而言
　
　
　
　
　
　
　
培养学生的观察能力和归纳能力
　
　
　
　
　
　
　
　
　
　
　
加深对中心对称基本性质的认识
　

(三)课堂练习，熟悉新知
　课文81页练习1、2
1、线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形、圆等图形中是轴对称图形的有___________________；是中心对称图形的有_________________；既是轴对称图形，又是中心对称的图形有__________．
　　 2、关于点M成中心对称的两个四边形ABCD和DEFG，AD、BE、CF、DG都过_______，并被点M所_______，AB∥______，BC∥_______，EF∥______，FG∥______．

(四)学习小结，自主评价
学生自主小结.学生交流在本节课学习中的体会、收获，交流学习过程中的体验与感受，以及可能存在的困惑，师生合作共同完成课堂小结.

培养学生归纳、概括问题的能力，引导学生反思学习过程

板书设计
　　　　　　　　　　　 15.3　中心对称(一)
　一、中心对称图形　　　　　　　　　　　三、两个图形关于某点对称的性质：
　　　对称中心：　　　　　　　　　　　　　 1、
　二、两个图形关于某点对称　　　　　　　　 2、
　　　对称中心：
　　　对应点：

试题详情

讲授式

试题详情

重点：中心对称图形的判定；

难点：中心对称图形和两个图形关于一点中心对称两个概念的区分.

试题详情

本课一开始直接展示一组轴对称图形，并提出问题，由问题引入数学新知识，从而激发学生研究问题、解决问题的欲望.

接着，让学生自己动手操作，直观地得出中心对称图形以及两个图形关于某点对称这两个概念，并加深对概念的理解.其间穿插展示一组来自生活实际中的、体现中心对称的图片，继续牢牢地吸引学生的注意力，体验中心对称图形在实际生活中的运用.

最后，借助演示，利用精心设计的一组问题，帮助学生掌握两个图形关于一点中心对称的概念、性质.