
1.必做题:教科书第193页习题15.4第1题(4);第2题;第3题;第4题;第5题;第6题.
15.4.2整式的除法
教学目标
①经历探索整式除法运算法则的过程,会进行简单的整式除法运算(只要求单项式除以单项式、多项式除以单项式,并且结果都是整式),培养学生独立思考、集体协作的能力.
②理解整式除法的算理,发展有条理的思考及表达能力.
教学重点与难点
重点:整式除法的运算法则及其运用.
难点:整式除法的运算法则的推导和理解,尤其是单项式除以单项式的运算法则.
教学准备
卡片及多媒体课件.
教学设计
情境引入
教科书第189页问题:木星的质量约为1.90×1024吨,地球的质量约为5.98×1021吨,你知道木星的质量约为地球质量的多少倍吗?
重点研究算式(1.90×1024)÷(5.98×1021)怎样进行计算,目的是给出下面两个单项式相除的模型.
***教科书从实际问题引入单项式的除法运算,学生在探索这个问题的过程中,将自然地体会到学习单项式的除法运算的必要性,了解数学与现实世界的联系,同时再次经历感受较大数据的过程.
探究新知
(1)计算(1.90×1024)÷(5.98×1021),说说你计算的根据是什么?
(2)你能利用(1)中的方法计算下列各式吗?
8a3÷2a; 6x3y÷3xy; 12a3b2x3÷3ab2.
(3)你能根据(2)说说单项式除以单项式的运算法则吗?
***教师可以鼓励学生自己发现系数、同底数幂的底数和指数发生的变化,并运用自己的语言进行描述.
单项式的除法法则的推导,应按从具体到一般的步骤进行.探究活动的安排,是使学生通过对具体的特例的计算,归纳出单项式的除法运算性质,并能运用乘除互逆的关系加以说明,也可类比分数的约分进行.在这些活动过程中,学生的化归、符号演算等代数推理能力和有条理的表达能力得到进一步发展.重视算理算法的渗透是新课标所强调的.
归纳法则
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
***通过总结法则,培养学生的概括能力,养成用数学语言表达自己想法的数学学习习惯.
应用新知
例2 计算:
(1)28x4y2÷7x3y;
(2)-5a5b3c÷15a4b.
首先指明28x4y2与7x3y分别是被除式与除式,在这儿省去了括号.对本例可以采用学生口述,教师板书的形式完成。口述和板书都应注意展示法则的应用,计算过程要详尽,使学生尽快熟悉法则.
***单项式除以单项式,既要对系数进行运算,又要对相同字母进行指数运算,同时对只在一个单项式里含有的幂要加以注意,这些对刚刚接触整式除法的学生来讲,难免会出现照看不全的情况,所以更应督促学生细心解答问题.
巩固新知 教科书第191页练习1及练习2.
学生自己尝试完成计算题,同桌交流.
***在独立解题和同伴的相互交流过程中让学生自己去体会法则、掌握法则,印象更为深刻,也有助于培养学生良好的思维习惯和主动参与学习的习惯.
再探新知计算下列各式:(1)(am+bm)÷m;(2)(a2+ab)÷a;(3)(4x2y+2xy2)÷2xy.①说说你是怎样计算的②还有什么发现吗?
在学生独立解决问题之后,及时引导学生反思自己的思维过程,并对自己计算所得的结果进行观察,总结出计算的一般方法和结果的项数特征:商式与被除式的项数相同.
***教科书提供了一些多项式除以单项式的题目,鼓励学生利用已经学习过的内容独立解决这些问题.教学中仍应提倡算法多样化,让学生说明每一步的理由,并鼓励学生间的交流.学生可以类比数的除法把除以单项式看成是乘以这个单项式的倒数,也可以利用逆运算进行考虑.
归纳法则
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
你能把这句话写成公式的形式吗?
***这里重要的是学生能理解运算法则及其探索过程,能够运用自己的语言叙述如何进行运算,不必要求学生背诵法则.用字母概括法则是使算法一般化,可深化和发展对数的认识.
解决问题
教科书第192页例3 计算
(1)(12a3-6a2+3a)÷3a;
(2)(21x4y3-35x3y2+7x2y2)÷(-7x2y);
(3)[(x+y)2-y(2x+y)-8x]÷2x
幂的运算性质是整式除法的关键,符号仍是运算中的重要问题.在此可由学生口答,要求学生说出式子每步变形的依据,并要求学生养成检验的习惯,利用乘除互为逆运算,检验商式的正确性.
***通过例题的剖析和解决,培养学生耐心细致、严谨的数学思维品质,训练学生形成一定的计算能力.
巩固新知教科书第192页练习利用投影仪反馈学生解题过程.
***本课课堂容量较大,可利用多媒体提高效率.
小结
回顾填写课堂评价表(见附页)
***评价表的填写,可以使学生全面地了解自己的学习过程,感受自己的成长与进步,这有利于培养学生的自信心,也为教师全面了解学生的学习状况、改进教学、实施因材施教提供了重要依据.
布置作业
5.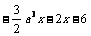 .
.
4.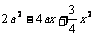 ;
;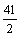 .
.
3.⑴4a2-2a+1;⑵-3xy2+5xy-y;⑶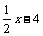 .
.
2.⑴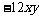 ;⑵
;⑵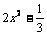 ;⑶
;⑶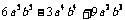 .
.
1.⑴D;⑵B;⑶C .
15.4.2整式的除法
同步训练
5.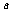 =1,或-1,或3.
=1,或-1,或3.
4.100.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com