
在学生学习了整式乘法和同底数幂相除法则之后安排整式的除法,由于新课标对整式除法的要求有所弱化,故本教材将单项式除以单项式、多项式除以单项式合为一节内容予以教学,并适当控制运算的难度。
3、“转化”的数学思想方法;
2、进行多项式混合运算要注意的三点。
(3)(9x2y-6xy2)÷(3xy) (4)(3x2y-xy2+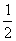 xy)÷(-
xy)÷(-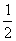 xy)
xy)
注意引导学生观察,思考:(1)商的项数与原多项式的项数相同;(2)多项式除以单项式实质是将其转化为单项式除以单项式,渗透转化的数学思想。
练习1、教材
练习2、1、填空:(1)(18a2b-9a3b2)÷(-3ab)=( )
(2)(9x3y4-6x4y3+3x2y3)÷( )=-3x2y2+2x3y-xy
(3)( )÷(-4x2)=-3x2 +4x-2
2、计算:(1)(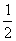 x3y3+4x2y2-3xy)÷(-3xy)
x3y3+4x2y2-3xy)÷(-3xy)
(2)(-2x2y2)3÷(-xy)3
(3)(a2+2ab+b2)÷(a+b)
(4)[20(a+b)2c+30(a+b)c2]÷[10(a+b)c]
例2、先化简,再求值:[(3x+4y)2-3x(3x+4y)]÷(-6y),其中x = -1,y = 3。
练习3、已知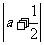 +(b-3)2 = 0,求代数式 [(2a+b)2-(2a+b)(2a-b)-6b]÷2b的值。
+(b-3)2 = 0,求代数式 [(2a+b)2-(2a+b)(2a-b)-6b]÷2b的值。
注意:(1)系数的符号;(2)灵活运用公式;(3)运算顺序。
总结:多项式除以单项式,先把多项式的每一项分别除以单项式,再把所得的商相加。
对照“做一做”中三题进行说明。
(1)(ad+bd)÷d (2)(a2b+3ab)÷a (3)(xy3-2xy)÷(xy)
(学生说出的理由可能有多种,只要合理就行。)
1、计算下列各题:(1)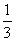 x3y4÷
x3y4÷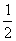 x3y2 (2)9a3b4c2÷2ab2÷3abc
x3y2 (2)9a3b4c2÷2ab2÷3abc
(3)(6×105)2÷(3×102)
1.规律的发现 2.方法的寻找 3.开放性的问题 4.知识的形成过程.本课的主要任务是完成单项式除以单项式法则的推导,继而将多项式除以单项式转化为单项式除以单项式,学生完全有能力通过探究,在原有的认知结构(熟悉分数的约分和幂的意义)基础上,建构整式的除法法则.同时,教师应重视引导,力求每个问题都是探索性的,引导他们自己发现,并且节奏紧凑,使学生的大脑一直处于兴奋状态,提高探究效率.
附:评价表(说明:在等级栏内打“√”)
|
内 容 |
自我评价 |
小组评价 |
||||
|
优 |
良好 |
需加油 |
优 |
良好 |
需加油 |
|
|
会推导单项式除以单项式的运算法则 |
|
|
|
|
|
|
|
会正确进行单项式除以单项式的运算 |
|
|
|
|
|
|
|
会正确进行多项式除以单项式的运算 |
|
|
|
|
|
|
|
能用代数形式概括多项式除以单项式的法则 |
|
|
|
|
|
|
|
本节课你所学到的数学方法 |
|
|||||
|
你认为在整式除法运算中应注意的问题 |
|
|||||
|
本节课你还有疑惑的问题 |
|
3.备选题:下列计算是否正确?如不正确;应怎样改正?
(1)-4ab2÷2ab=2b (2)(14a3-2a2+a)÷a=14a2-2a
***易错题、改错题可以培养运算能力,加深对法则的理解.
设计思想
《数学课程标准》强调:要让学生经历知识的形成与应用的过程.通过课堂学习,我们不应只关心学生记住了多少性质,背出了几个公式,更应关注的是学生是否参与了知识的发现、形成过程,并从中体验成功的喜悦,掌握学习策略,发展能力.所以本节课我采用“自主探究性学习”.“自主探究性学习”是以学生自主探究为主的教学方式,在实践中我认为这样一些内容可以采用此教学方式:
2.选做题:教科书第193页习题15.4第8题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com