
2.下列计算正确的是( )
A.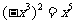 ; B.
; B.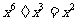 ;C.
;C.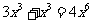 D.
D.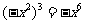
1、若(am+1bn+1)(a2nb2m)=a5b3,则m+n的值为( )
A、1 B、2 C、3 D、-3
5. 若x2+2(k-3)x+25是一个完全平方式,则k的值是____________
[模拟试题]
4、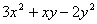
3.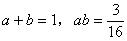 已知
,求
已知
,求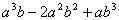 的值。
的值。
[例]因式分解: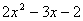
解:首项2可拆成1与2尾项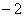 可拆成
可拆成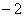 与1
与1
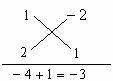
∴ 原式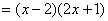
2、分解(1)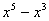 (2)
(2)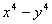
[典型例题]
例1. 求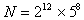 是几位正整数。
是几位正整数。
例2. 已知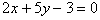 ,求
,求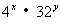 的值。
的值。
例3. 已知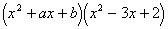 中不含
中不含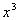 和
和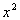 项,求a、b的值。
项,求a、b的值。
分析:不含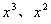 项就是说按多项式乘法法则展开,再合并同类项后,式子中
项就是说按多项式乘法法则展开,再合并同类项后,式子中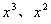 项的系数为0,故本题可先将多项式按多项式乘法法则展开,合并同类项,然后令
项的系数为0,故本题可先将多项式按多项式乘法法则展开,合并同类项,然后令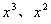 项的系数为0,得到关于a、b的方程组,从而通过解方程组求出a、b的值。
项的系数为0,得到关于a、b的方程组,从而通过解方程组求出a、b的值。
解答: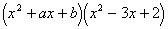
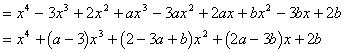
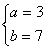 根据题意得:
根据题意得: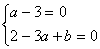
例4.计算: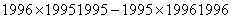
例5.分解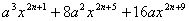
例6. 设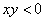 ,要使
,要使
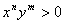 那么(
)
那么(
)
A. 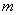 、
、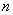 都应为偶数
B.
都应为偶数
B. 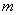 、
、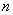 都应是奇数
都应是奇数
C. 无论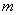 、
、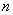 为奇数或偶数都可以
D. 无论
为奇数或偶数都可以
D. 无论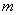 、
、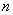 为奇数或偶数都不行
为奇数或偶数都不行
[易错整理]
1、若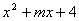 是一个完全平方式,求
是一个完全平方式,求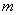 ?
?
(1)如果多项式的某一项恰好就是公因式时,提公因式后另一个因式中商为“1”的这一项不能漏掉,应使另一个因式的项数与原多项式的项数相同。
(2)如果多项式的首项的系数为负,在分解因式时一般要提出“-”号,此时,括号内的各项都要变号;
(3)当公因式是多项式时,除了要注意符号问题外,还要注意提公因式后另一个因式还要进行整理,化简,如果有公因式还要提取,并且相同的因式要写成幂的形式
2、理解整式除法运算的算理,发展有条理的思考及表达能力。
[教学重点、难点]
重点是会利用单项式除以单项式法则和多项式除以单项式法则,进行简单的整式除法运算。
难点是全面、准确地理解二个法则。
[教学准备]
展示课件。
[教学过程]
|
教学过程 |
设计说明 |
|
一、回顾与思考 复习整式乘法中单项式乘以单项式、多项式乘以多项式和同底数幂相除法则。 二、合作学习,探求新知 1、合作学习 月球是距离地球最近的天体,它与地球的距离约为3.8×108米,如果宇宙飞船以1.12×104米/秒的速度飞行,到达月球大约需要多少时间? 2、探求新知 解决上述问题时,你是怎样计算的? 由此你能找到计算(3a8)÷(2a4)的方法吗? 计算(6a3b4)÷(3a2b)呢? 3、议一议: 一般地,两个单项式相除,可以转化为系数与系数相除以及同底数幂的相除,例如: 14·a3·a2·x (14a3b2x)÷(4ab2)= ------ 4·a·b2 7 7 = - a3-1·b2-2·x= - a2x 2 2 议一议:如何进行单项式除以单项式的运算? 法则:单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。 三、应用新知,体验成功 1、试一试: 4 计算:(1)-a7x4y3÷(-- ax4y2) 3 (2)2a2b·(-3b2)÷(4ab3) (3)(2a+b)4÷(2a+b)2 2、辨一辨: (1)(12a3b3c)÷(6ab2)=2ab (2)(p5q4)÷(2p3q)=2p2q3 3、练一练: 计算与填空 ①(10ab3)÷(5b2)= ②3a2÷(6a6)·(-2a4)= ③( )·3ab2=-9ab5 ④(-12a3bc)÷( )=4a2b 四、探究延伸,再会新知 1、做一做 先填空,再用适当的方法验证计算的正确性。 (1)(625+125+50)÷25 =( )÷( )+( )÷( )+( )÷( ) = (2)(4a+6)÷2=( )÷( )+( )÷( ) = (3)(2a-a)÷(-2a) =( )÷(-2a)+( )÷(-2a) = 2、议一议 从上述第(2)、(3)题的计算中,你能归纳出多项式除以单项式的运算方法吗? 法则:多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。 即:(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0) 3、试一试 计算 (1)(14a3-7a2)÷(7a) (2)(15x3y5-10x4y4-20x3y2)÷(-5x3y2) 4、练一练 (1)辨别正误: ①(am+bm+cm2)÷m=a+b+c ②(2x-4y+3)÷2=x-2y+3 (2)计算式填空 ①(15x2y-10xy2)÷(5xy) ②(4c3d2-6c2d3)÷(-3c2d) ③ [3a2-( )]÷(-a)=-3a+2b ④( )·(-2y)=4x2y-6xy2 五、归纳小结、充实结构  1、单项式相除 (1)系数相除 1、单项式相除 (1)系数相除(2)同底数幂相除 (3)只在被除式里的幂不变 2、多项式除以多项式 先把这个多项式的每一项分别除以单项式,再把所得的商相加。 六、知识留恋、课后韵味 课外作业:课本后附作业题 |
复习学过的知识或回顾有关联的内容,对新知识的探究和学习是十分必要的,它可以引发对新知的探究。 合作学习是在独立学习时,学生有解决不了的问题需大家共同交流、合作的小组式的学习,合作学习能达到有效沟通、激活思维、提高参与度等作用。 学生类比数的运算,自然会想到整式除法的运算应该如何进行。 在前面合作交流的基础上,让学生自己概括出单项式除以单项式的运算法则。 重要的是理解法则及其探索过程中,尽可能用自己的语言叙述如何进行运算,不必要求学生背诵法则。 设置(3),鼓励学生自己悟出:将{2a+b}视为一个整体来进行运算。 辨中弄清概念 多种形式的题目来巩固运算法则,并及时反馈。 由数类比到代数式体现由特殊到一般,再由一般到特殊,通过学生自己做一做,有力于知识的自主构建。 议的过程是一个探究、归纳的过程。 通过例题探究加点拨、练习、辨别等多形式、多渠道的巩固训练,充分应用新知来解决问题。 通过小结,及时地将新知识纳入已有的知识体系中,充实自己的数学知识结构。 |
[设计说明]
本节课所要掌握的内容更多,包括单项式相除和多项式除以单项式二个法则,故本节设计采用二段论式,将有利于学生对知识的掌握,通过复习旧知,合作学习,类比迁移而得到二个法则,在设计中和授课时最大可能地让学生参与到自主学习、合作学习与探究学习中。
[教学内容分析]
本节课学习单项式除以单项式法则和多项式除以单项式法则,即是对整式乘法和同底数幂相除法则的复习,又有新知识的学习。
[教学目标]
1、经历探索整式除法运算法则的过程,会进行简单的整式除法运算(只要求单项式除以单项式、多项式除以单项式,并且结果都是整式)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com