6．P26思考提出问题，让学生思考用负整数指数幂来表示小于1的数，从而归纳出：对于一个小于1的数，如果小数点后至第一个非0数字前有几个0，用科学计数法表示这个数时，10的指数就是负几.

5．P25最后一段是介绍会用科学计数法表示小于1的数. 用科学计算法表示小于1的数，运用了负整数指数幂的知识. 用科学计数法不仅可以表示小于1的正数，也可以表示一个负数.

4． P25例10判断下列等式是否正确？是为了类比负数的引入后使减法转化为加法，而得到负指数幂的引入可以使除法转化为乘法这个结论，从而使分式的运算与整式的运算统一起来.

3． P24例9计算是应用推广后的整数指数幂的运算性质，教师不要因为这部分知识已经讲过，就认为学生已经掌握，要注意学生计算时的问题，及时矫正，以达到学生掌握整数指数幂的运算的教学目的.

2． P24观察是为了引出同底数的幂的乘法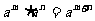：，这条性质适用于m,n是任意整数的结论,说明正整数指数幂的运算性质具有延续性.其它的正整数指数幂的运算性质，在整数范围里也都适用.

1． P23思考提出问题，引出本节课的主要内容负整数指数幂的运算性质.

3．认知难点与突破方法

复习已学过的正整数指数幂的运算性质：

(1)同底数的幂的乘法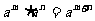：(m,n是正整数)；

(2)幂的乘方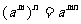：(m,n是正整数)；

(3)积的乘方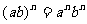：(n是正整数)；

(4)同底数的幂的除法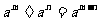：( a≠0，m,n是正整数，

m＞n)；

(5)商的乘方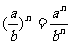：(n是正整数)；

0指数幂，即当a≠0时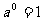，. 在学习有理数时，曾经介绍过1纳米=10^-9米，即1纳米=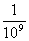米.此处出现了负指数幂，也出现了它的另外一种形式是正指数的倒数形式，但是这只是一种简单的介绍知识，而没有讲负指数幂的运算法则.

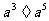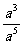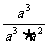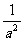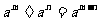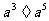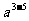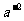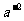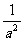学生在已经回忆起以上知识的基础上，一方面由分式的除法约分可知，当a≠0时，===；另一方面，若把正整数指数幂的运算性质(a≠0，m,n是正整数，m＞n)中的m＞n这个条件去掉，那么==.于是得到=(a≠0)，就规定负整数指数幂的运算性质：当n是正整数时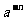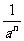，=(a≠0)，也就是把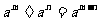的适用范围扩大了，这个运算性质适用于m、n可以是全体整数.

2．难点：会用科学计数法表示小于1的数.

1．重点：掌握整数指数幂的运算性质.

3．会用科学计数法表示小于1的数.