0．000 04，　 -0. 034,　　 0.000 000 45,　　 0. 003 009

1. 用科学计数法表示下列各数：

2.计算

(1) (x³y^-2)²　　 (2)x²y^-2 ·(x^-2y)³(3)(3x²y^-2) ² ÷(x^-2y)³

1.填空

(1)-2²=　　　　 (2)(-2)²=　　　　 (3)(-2) ⁰=　　　　 

(4)2⁰=　　　　　 　　( 5)2 ^-3=　　　　　 　( 6)(-2) ^-3=　　　　

(P24)例9.计算

[分析] 是应用推广后的整数指数幂的运算性质进行计算，与用正整数

指数幂的运算性质进行计算一样，但计算结果有负指数幂时，要写成分式形式.

(P25)例10. 判断下列等式是否正确？

[分析] 类比负数的引入后使减法转化为加法，而得到负指数幂的引入可以使除法转化为乘法这个结论，从而使分式的运算与整式的运算统一起来，然后再判断下列等式是否正确.

(P26)例11.

[分析] 是一个介绍纳米的应用题，是应用科学计数法表示小于1的数.

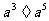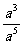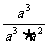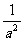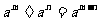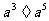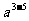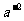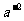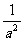4．计算当a≠0时，===，再假设正整数指数幂的运算性质(a≠0，m,n是正整数，m＞n)中的m＞n这个条件去掉，那么==.于是得到=(a≠0)，就规定负整数指数幂的运算性质：当n是正整数时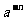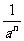，=(a≠0).

3．你还记得1纳米=10^-9米，即1纳米=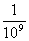米吗？

2．回忆0指数幂的规定，即当a≠0时，.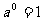

1．回忆正整数指数幂的运算性质：

(1)同底数的幂的乘法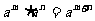：(m,n是正整数)；

(2)幂的乘方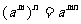：(m,n是正整数)；

(3)积的乘方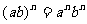：(n是正整数)；

(4)同底数的幂的除法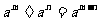：( a≠0，m,n是正整数，

m＞n)；

(5)商的乘方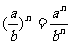：(n是正整数)；

7．P26例11是一个介绍纳米的应用题，使学生做过这道题后对纳米有一个新的认识.更主要的是应用用科学计数法表示小于1的数.