
5.分式的运算.
4.分式的通分:即要求把几个异分母的分式分别化成与原来分式值相等的同分母的分式.
通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂作为公分母,叫做最简公分母,确定最简公分母的办法:(1)系数取最小公倍数;(2)字母取所有字母;(3)取所有字母的最高次幂,特别注意:为了确定最简公分母,通常先将各分母分解因式.
3.分式的约分:分式的分子和分母都同除以分子和分母的公因式.
确定公因式的方法:(1)取分子和分母系数最大公约数;(2)字母取分子和分母中相同字母;(3)相同字母取最低次幂.
如果分子和分母是多项式,则先将多项式分解因式,才能容易发现和约去分子和分母中的公因式,将分式化为最简分式.
2.分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式值不变,用式子表示为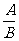 =
=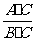 ,
,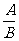 =
=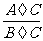 (C是整式,且C≠0).
(C是整式,且C≠0).
1.分式概念: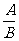 式子中A、B都是整式,B中含有字母,且B≠0.
式子中A、B都是整式,B中含有字母,且B≠0.
11. 解:a2-4a+9b2+6b+5=0得,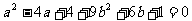 ,则(
,则(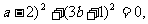 则
则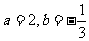 ,代入得3
,代入得3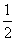 .
.
原式=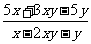 =
=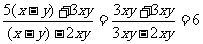
10.解:由 知
知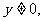 ∴
∴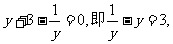
∴(
∴(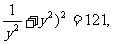 ∴
∴ 由
由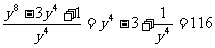 ,
,
∴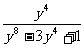 =
=
8. 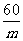 (答案不唯一);
(答案不唯一);
7.10,99,提示:从前面的式子得到规律:分子是加号前面的数,分母是分子的平方减1,故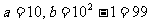 ;
;
6.3.提示:分式的值为零就是分子等于零且分母不等于零即为
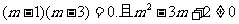 ,解得
,解得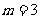 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com