
7.计算:
6.计算: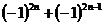 =______________(n为整数)
=______________(n为整数)
4.若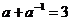 ,则
,则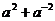 等于( )
等于( )
A. 9 B. 1 C. 7 D. 11
5已知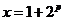 ,
,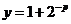 ,则用x表示y的结果是( )
,则用x表示y的结果是( )
A. 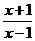 B.
B.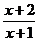 C.
C.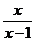 D.
D.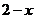
3.若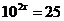 ,则
,则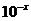 等于( )
等于( )
A.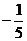 B.
B.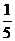 C.
C.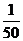 D.
D.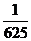
2.下列计算正确的是( )
A.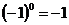 B.
B.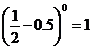 C.
C. 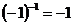 D.
D.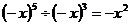
1.若m,n为正整数,则下列各式错误的是( )
A.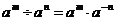 B.
B.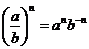 C.
C.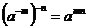 D.
D. 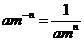
16.2.3 整数指数幂(1)
 知识领航:
知识领航:
任何一个不等于零的数的零次幂等于1, 即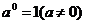
当n为正整数时,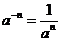 (
(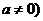
正整数指数幂运算性质也可以推广到整数指数幂.
 e线聚焦
e线聚焦
[例] 计算:(1)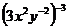 , (2)
, (2)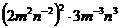 .
.
分析:可先运用幂的运算性质进行计算,再化成正整数指数的形式.
解:(1)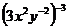 =
=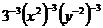 =
=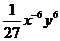 =
=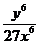 .
.
(2)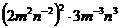 =
=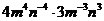 =
=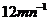 =
=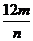 .
.
 双基淘宝
双基淘宝
◆仔细读题,一定要选择最佳答案哟!
4.( )-1= 3 (- )-3 = -125 . 5.计算(3×4-24×0.5)0是 (D) A.0 B.1 C.24 D.无意义 二、提升能力 6.已知5x-3y+2=0,求105x÷103y的值 [答案] 0.01 三、开放探究 7.已知3m=5,3-n=4,求32m+n-1的值.
16.2.3 整数指数幂
教学目标
1.知识与技能
理解负指数幂的性质,正确熟练地运用负指数幂公式进行计算,会用科学记数法表示绝对值较小的数.
2.过程与方法
通过幂指数扩展到全体整数,培养学生抽象的数学思维能力,运用公式进行计算,培养学生综合解题的能力和计算能力.
3.情感、态度与价值观
在数学公式中渗透公式的简洁美、和谐美,随着学习的知识范围的扩展,产生对新知识的渴望与追求的积极情感,让学生形成辩证统一的哲学观和世界观.
教学重点难点
重点:理解和应用负整数指数幂的性质,用科学记数法表示绝对值较小的数.
难点:负整数指数幂公式中字母的取值范围,用科学记数法表示绝对值较小的数时,a×10n形式中n的取值与小数中零的关系.
课时安排 2课时
第1课时
(一)创设情境,导入新课
提问 (投影显示)(1)同底数幂除法公式am÷an=am-n中m、n有什么条件限制吗?
(2)若a0=1,则a ≠0 .
(3)计算52÷55= 5-3 ,103÷107= 10-4 .
(二)合作交流,解读探究
做一做 你发现了什么?
一方面:(1)52÷55=52-5=5-3
(2)103÷107=103-7=10-4
另一方面:(1)52÷55= (2)103÷107= 则5-3= 10-4=
归纳 请总结一般规律.
一般地,规定:a-n= (a≠0,n是正整数),即任何不等于零的数的-n(n为任何正整数)次幂,等于这个数的n次幂的倒数.
议一议 为什么公式中规定a≠0?
试一试 求下列各式值.
(1)5-3= (2)2-2=
(3)a-1= (a≠0) (4)(2x)-2=
(三)应用迁移,巩固提高
例1计算:(1)3-3; (2)(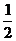 )-2; (3)(
)-2; (3)(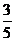 )0×10-1.
解:(1)3-3= ; (2)(
)0×10-1.
解:(1)3-3= ; (2)(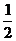 )-2= =4;
(3)(
)-2= =4;
(3)(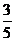 )0×10-1=1×
)0×10-1=1× 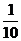 =
例2计算:(1)(-2)-2; (2)(-2)-3; (3)(-a)-2; (4)(-a)-5.
解:(1)(-2)-2= ; (2)(-2)-3= ;
(3)(-a)-2=; (4)(-a)-5=.
想一想 例2的解题过程中你发现什么规律?
议一议 我们引进了零指数和负整数指数幂,指数的范围已经扩大到了全体整数,那么以前所学的幂的性质是否成立呢?
例3判断下列式是否成立
(1)a2·a-3=a2+(-3) ( )
=
例2计算:(1)(-2)-2; (2)(-2)-3; (3)(-a)-2; (4)(-a)-5.
解:(1)(-2)-2= ; (2)(-2)-3= ;
(3)(-a)-2=; (4)(-a)-5=.
想一想 例2的解题过程中你发现什么规律?
议一议 我们引进了零指数和负整数指数幂,指数的范围已经扩大到了全体整数,那么以前所学的幂的性质是否成立呢?
例3判断下列式是否成立
(1)a2·a-3=a2+(-3) ( )
(2)(ab)-3=a-3b-3 ( ) (3)(a-3)2=a(-3×2) ( ) 解:(1)、(2)、(3)都成立. 例4计算:
(1)(-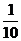 )-3+(
)-3+(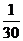 )-2×3.140-(-3)3×3+(-
)-2×3.140-(-3)3×3+(-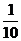 )-2;
(2)(3m-1n2)-2(m2n-3)-3;
(3)(-8×10-6)2÷(2×10-3)2
解:(1)原式=-1 000+900×1-(-27)+100
=-1 000+900+27+100
=27
)-2;
(2)(3m-1n2)-2(m2n-3)-3;
(3)(-8×10-6)2÷(2×10-3)2
解:(1)原式=-1 000+900×1-(-27)+100
=-1 000+900+27+100
=27
(2)原式=(3-2m+2n-4)(m-6n9)
=3-2m-4n5
(3)原式=(64×10-12)÷(4×10-6)
=16×10-6
=1.6×10-5
(四)总结反思,拓展升华
综合运用幂的运算法则进行计算,先做乘方,再做乘除,最后做加减,若遇括号,应做括号内的运算;对于底数是分数的负整数指数幂,可先颠倒分数的分子和分母的位置,便可把负整数指数化为已知整数指数:如:( 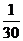 )-2=302,0.3-1=(
)-2=302,0.3-1=(  )-1=
)-1= 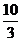 (五)课堂跟踪反馈
一、夯实基础
1.(-3)0= 1 5-2=
2.若(5x-10)0=1,则成立条件为 x≠2
3.若式子(x2-3x+2)-5有意义,则x的取值范围 x≠2且x≠1
(五)课堂跟踪反馈
一、夯实基础
1.(-3)0= 1 5-2=
2.若(5x-10)0=1,则成立条件为 x≠2
3.若式子(x2-3x+2)-5有意义,则x的取值范围 x≠2且x≠1
15.纳米技术是21世纪的新兴技术,1纳米等于10-9米,已知某花粉的直径为35000纳米,用科学记数法表示此种花粉的直径是多少米?
[答案] 3.5×10-5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com