3．如图，梯形ABCD中,AD∥BC，∠B=70°，∠C=40°，试说明CD=BC-AD。

根据学生解题的实际情况及时反馈纠正。

2．填空。　　

　　 如图，等腰梯形ABCD中，AD∥BC，∠B=60°，AB=8厘米，则

　　 (1)∠C=(　 )，∠D=(　 )，CD=(　 )厘米。

(2)若BC=15厘米，则AD=(　 )厘米，梯形面积S=(　 )厘米²。

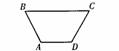
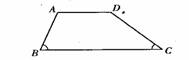
　　　　 第2题　　　　　　　　　　 　第3题

　　 上面探索发现的结论经过推理都是正确的，今后我们可利用这些结论进行有关计算与证明。

1．判断。

　　 (1)一组对边平行的四边形是梯形。　　 (　　 )

　　 (2)一组对边平行且相等的四边形是梯形。　　 (　　 )

5．思考讨论

　　 我们在探索证明的过程中，得到的解决梯形问题的一般方法是什么?

(板书。)梯形转化三角形和平行四边形。

4．等腰梯形的特征的发现及证明。

　　 等腰梯形是我们常见的图形，利用它的特殊形状可以构造各种建筑模　 型，设计各种图案，比如我们常用的梯子。下面观察演示一下等腰梯形具有哪些特征?

　　 让学生先在硬纸片上画一个等腰梯形，再用剪刀剪下来，通过折叠、对比、演示，启发学生从腰、底角、对角线的对称性人手，寻求发现等腰梯形的特征，培养学生观察、分析、概括的能力。

　　 让学生试述结论，教师适时用准备好的等腰梯形纸片进行演示并及时　 补充完善结论。

　　 等腰梯形的性质：

　　 (1)两腰相等；(2)同一底上两角相等；(3)两条对角线相等；(4)轴对

　 称图形，对称轴是过两底中点的直线。

　　 (性质(4)，学生不易发现，应引导他们联系等腰三角形的轴对称性发现

　 结论并叙述。)

　　 同学们经过努力，发现了上述结论，这些结论是否成立仅靠观察是不可靠的，需要用所学知识进行严密的推理论证。(教师应引导学生积极探求真理，激发学生的求知欲，由小组讨论、探索证明思路。教师启发点拔，怎样添加辅助线使梯形转化成已熟悉的三角形和平行四边形?通过启发引导学生利用转化思想解决问题。)

可让学生广开思路，任其发挥，教师根据学生的推理情况调控教学。对于结论(2)若学生运用转化思想，能找出证明思路，应给予充分的肯定和鼓励。由学生口述教师板书完整的证明过程；若不能的，引导学生做如下探索推证。　　

如图，梯形ABCD中，AD∥BC，AB=CD，请你说明∠B=∠C。

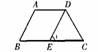
3．特殊梯形。

　　 观察图(4)和图(5)的特点，找出它们与一般梯形的区别，引导得出直角梯形和等腰梯形的概念。由学生试述，教师根据回答情况及时更正并板书。　　 (板书。)一腰垂直于底的梯形叫做直角梯形。两腰相等的梯形叫做等腰梯形。特殊梯形直角梯形等腰梯形

　　 思考讨论：若上面两个条件同时成立是否是梯形?

l.如图，梯形ABCD中，AD∥BC，上底是______下底是______，并作出高。

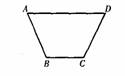
2．小组讨论。

　　 (1)一组对边平行的四边形是梯形吗?

(2)一组对边平行且相等的四边形是梯形吗?

　　 让学生观察图(3)，并跟平行四边形的定义进行对比，引导学生试述梯形的概念，并结合图形说出梯形的底、腰及高。

　　 (板书。)一组对边平行，另一组对边不平行的四边形叫做梯形。(或：只有一组对边平行的四边形叫做梯形。)

如图，梯形ABCD中，AD∥BC，其中AD是上底，BC是下底，AB、CD是腰，EF是高。

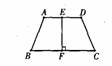
2．学生回答后在图(2)旁边标注“对边平行”，然后指向图(3)，同图 (3)是什么四边形?学生回答后板书课题：梯形。

1．说出平行四边形的特征与其识别的方法。

观察图形。