2．教学难点：检验分式方程解的原因

1．教学重点：

(1)可化为一元一次方程的分式方程的解法．

(2)分式方程转化为整式方程的方法及其中的转化思想．

5．通过学习分式方程的解法，使学生理解解分式方程的基本思想是把分式方程转化成整式方程，把未知问题转化成已知问题，从而渗透数学的转化思想．

4．在学生掌握了分式方程的一般解法和分式方程验根方法的基础上，使学生进一步掌握可化为一元一次方程的分式方程的解法，使学生熟练掌握解分式方程的技巧．

3．了解解分式方程解的检验方法．

2．使学生掌握可化为一元一次方程的分式方程的一般解法．

1．使学生理解分式方程的意义．

4、学习小结

　本节课你学到了哪些知识？有什么感想？

3、随堂练习

　(1)据联合国《2003年全球投资报告》指出，中国2002年吸收外国投资额达530亿美元，比上一年增加了13%．设2001年我国吸收外国投资额为亿美元，请你写出满足的方程．你能写出几个方程？其中哪一个是分式方程？

　(2)轮船在顺水中航行20千米与逆水航行10千米所用时间相同，水流速度为2.5千米/小时，求轮船的静水速度．

　(3)为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等．如果设第一次捐款人数为x人，那么x满足怎样的方程？

　(4)　　　　　　　　 　　　　　　　　　

　(5)

2、解读探究

　(1)从甲地到乙地有两条公路：一条是全长600km的普通公路，另一条是全长480km的高速公路．某客车在高速公路上行驶的平均速度比在普通公路上快45km/h，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半．求该客车由高速公路从甲地到乙地所需的时间．

　这一问题中有哪些等量关系？

　如果设客车由高速公路从甲地到乙地所需的时间为xh，那么它由普通公路从甲地到乙地所需的时间为_________h．根据题意，可得方程_________________．

　学生分组探讨、交流，列出方程.

　等量关系：

　①客车在高速公路上行驶的平均速度=在普通公路上的平均速度+45；

　②由高速公路从甲地到乙地所需的时间×2=由普通公路从甲地到乙地所需的时间

　方程：=+45

　(2)王军同学准备在课外活动时间组织部分同学参加电脑网络培训，按原定的人数估计共需费用300元；后因人数增加到原定人数的2倍，费用享受了优惠，一共只需要480元，参加活动的每个同学平均分摊的费用比原计划少4元；原定的人数是多少？

　你能找出这一问题中所有的等量关系吗？

　如果设原定是x人，那么每人平均分摊________元；

　人数增加到原定人数的2倍后，每人平均分摊________元；

　根据题意，可得方程________

　议一议：

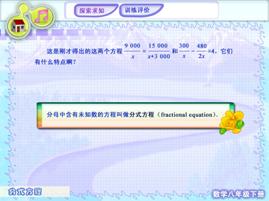
　上面所得到的方程有什么共同特点？

　分母中含有未知数的方程叫做分式方程．

　分式方程与整式方程有什么区别？

　做一做：

　解方程：=

　解：方程左右两边都乘以x(x−2)，得

　x = 3(x−2)，解这个方程，得x = 3

　检验：将x = 3代入原方程，得，左边 = 1 = 右边

　所以x = 3是原方程的解．

　这里为什么要检验呢？

　在解方程=−2时，有人这样解：

　方程两边都乘以x−3，得

　2−x = −1−2(x−3)，解这个方程，得x = 3

　在这里x = 3不是原方程的解，因为它使原分式方程的分母为0

　因此，在解分式方程时，在解得结果后需要检验

　归纳解分式方程的一般步骤：

　①去分母，转化为整式方程

　②解整式方程，得出整式方程的解

　③检验；将整式方程的解代入到原分式方程的最简公分母中，若最简公分母不为0，则该整式方程的解是原分式方程的解，反之，若最简公分母为0，则该整式方程的解不是原分式方程的解．