(1)为什么要检验根？

在将分式方程变形为整式方程时，方程两边同乘以一个含未知数的整式，并约去了分母，有时可能产生不适合原分式方程的解(或根).对于原分式方程的解来说，必须要求使方程中各分式的分母的值均不为零，但变形后得到的整式方程则没有这个要求.如果所得整式方程的某个根，使原分式方程中至少有一个分式的分母的值为零，也就是说使变形时所乘的整式(各分式的最简公分母)的值为零，它就不适合原方程，则不是原方程的解.

(2)验根的方法

一般的，解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为0，因此应如下检验：

将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解，否则，这个解不是原分式方程的解.

解方程：

(1)　

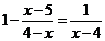
解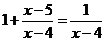： 　　　　方程两边同乘以 ，

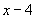得　 ．　　　　 ∴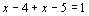 　　

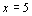
检验：把x=5代入 x-5，得x-5≠0

所以，x=5是原方程的解.

(2)

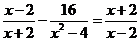
解：方程两边同乘以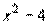 ，得

　　　　 　　，　　 ∴ ．

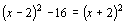
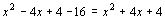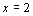检验：把x=2代入 x²-4，得x²-4=0.

所以，原方程无解..

思考：上面两个分式方程中，为什么(1)去分母后所得整式方程的解就是(1)的解，而(2)去分母后所得整式的解却不是(2)的解呢？

学生活动：小组讨论后总结

(五)练习

补充练习：

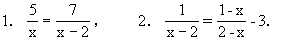
解1：方程两边同乘x(x-2)，

5(x-2)=7x

5x-10=7x

2x=10

x=5．

检验：把x=-5代入最简公分母

x(x-2)≠0，

∴x=-5是原方程的解．

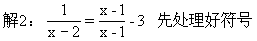
方程两边同乘最简公分母(x-2)，

1=x-1-3(x-2)．　　　　　　　　　　 (-3这项不要忘乘)

1=x-1-3x+6

2x=4

x=2．

检验：把x=2代入最简公分母(x-2)=0，

∴原方程无解．

(四)总结

解分式方程的一般步骤：

1．在方程的两边都乘以最简公分母，约去分母，化为整式方程．

2．解这个方程．

3．把整式方程的根代入最简公分母，看结果是不是零；使最简公分母为零的根不是原方程的解，必须舍去．

(三)　 应用

一艘轮船在静水中的最大航速为20千米/时，它沿江以最大航速顺流航行100千米所用的时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？

分析：设江水的流速为v千米/时，

则轮船顺流航行的速度为(20+v)千米/时，逆流航行的速度为(20－v)千米/时，顺流航行100千米所用的时间为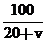小时，逆流航行60千米所用的时间为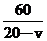小时。

可列方程＝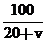

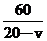
解方程得：v＝5

检验：v＝5为方程的解。

所以水流速度为5千米/时。

(二)新课

板书课题：

板书：分式方程的定义．

分母里含有未知数的方程叫分式方程．以前学过的方程都是整式方程．

练习：判断下列各式哪个是分式方程．

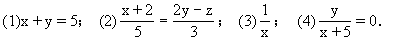
在学生回答的基础上指出(1)、(2)是整式方程，(3)是分式，(4)是分式方程．

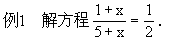
先由同学讨论如何解这个方程．

在同学讨论的基础上分析：由于我们比较熟悉整式方程的解法，所以要把分式方程转化为整式方程，其关键是去掉含有未知数的分母．

解：两边同乘以最简公分母2(x+5)得

2(x+1)=5+x

2x+2=5+x

x=3．

如果我们想检验一下这种方法，就需要检验一下所求出的数是不是方程的解．

检验：把x=3代入原方程

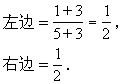
左边=右边

∴x=3是原方程的解．

(一)复习及引入新课

1．提问：什么叫方程？什么叫方程的解？

答：含有未知数的等式叫做方程．

使方程两边相等的未知数的值，叫做方程的解．

解：(1)当x=0时，

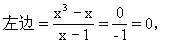
右边=0，

∴左边=右边，

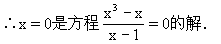
这个方程和我们以前所见过的方程不同，它的主要特点是：分母中含有未知数，这种方程就是我们今天要研究的分式方程．

演示法和同学练习相结合，以练习为主．

启发式设问和同学讨论相结合，使同学在讨论中解决问题，掌握分式方程解法．

3．疑点及分析和解决办法：

解分式方程的基本思想是将分式方程转化为整式方程(转化思想)，基本方法是去分母(方程左右两边同乘最简公分母)，而正是这一步有可能使方程产生增根．让学生在学习中讨论从而理解、掌握．