新的课程标要求“让学生经历数学知识的形成与应用过程，鼓励学生自主探索与合作交流”。本节课采用教师为主导、学生为主体、练习为主线的教学策略，教师的作用主要体现在创设合适的问题情境，引导学生在课堂上发挥主观能动性，体现学生的主体地位，练习是学生学习数学知识和掌握数学能力的平台，因此把练习教学当成一节课的主线。

(二)教学目标

知识与技能：

1、掌握梯形、直角梯形、等腰梯形的有关概念；探索并掌握等腰梯形的性质。

2、通过把梯形问题转化为三角形或平行四边形的问题，体会数学的转化思想。

3、能运用梯形的性质进行相关计算和简单的说理。

过程与方法：

1、经历探索等腰梯形的性质过程，培养学生的动手操作能力、观察能力、说理意识,提高解决问题的能力。

　2、经历探索把梯形问题转化为三角形和平形四边形问题，培养学生的创新意识，体会数学转化思想。

情感态度价值观：

在合作探索、自主学习的过程中，让学生体验数学学习活动充满探索性、创造性和趣味性，培养学生学习数学的热情和自信心。

重点：

1、梯形的性质及其应用。

2、会把梯形问题转化为三角形或平行四过形问题。

难点：

发展合情推理能力和主动探究习惯，提高说理的表达能力。

(四)小结

对于列方程解应用题，一定要善于把生活语言转化为数学语言，从中找出等量关系．对于我们常见的几种类型题我们要熟悉它们的基本关系式．

(三)课堂练习

课本P37 1.2

补充练习：

1．、乙分别从相距36千米的A、B两地同时相向而行．甲从A出发到1千米时发现有东西遗忘在A地，立即返回，取过东西后又立即从A向B行进，这样二人恰好在AB中点处相遇，又知甲比乙每小时多走0.5千米，求二人速度．

根据题意，得

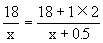
解得　 x=4.5．

经检验，x=4.5是这方程的解．

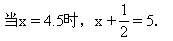
答：甲速度为5千米/小时，乙速度为4.5千米/小时．

(二)新课

例3．两个工程队共同参加一项筑路工程，甲队单独施工1个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。哪个队的施工速度快？

分析：甲队一个月完成总工程的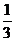，设乙队如果单独施工1个月能完成总工程的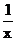，那么甲队半个月完成总工程的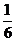，乙队半个月完成总工程的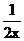，两队半个月完成总工程的+。

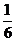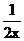等量关系为：甲、乙两个工程总量＝总工程量

则有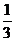++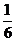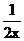＝1

(教师板书解答、检验过程)

例4：

从2004年5月起某列列车平均提速v千米/时。用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度是多少？

分析：这里的字母v，s表示已知数据，设提速前的平均速度为x千米/时，则

提速前列车行驶s千米所用的时间为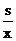小时，提速后列车的平均速度为(x+v)千米/时，提速后列车行驶(s+50)千米所用 的时间为小时。

等量关系：提速前行驶50千米所用的时间＝提速后行驶(s+50)千米所用的时间

列方程得：

＝

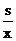(教师板书解答、检验过程)

(一)复习提问

1．解分式方程的步骤

(1)能化简的先化简；(2)方程两边同乘以最简公分母，化分式方程为整式方程；(3)解整式方程；(4)验根．

2．列方程应用题的步骤是什么？

(1)审；(2)设；(3)列；(4)解；(5)答．

3．由学生讨论，我们现在所学过的应用题有几种类型？每种类型题的基本公式是什么？

在学生讨论的基础上，教师归纳总结基本上有五种：

(1)行程问题：基本公式：路程=速度×时间

而行程问题中又分相遇问题、追及问题．

(2)数字问题

在数字问题中要掌握十进制数的表示法．

(3)工程问题

基本公式：工作量=工时×工效．

　(4)顺水逆水问题

v_顺水=v_静水+v_水．

v_逆水=v_静水-v_水．

课本P35　

化简，得

　　　　　　　　 x+2＝3

解得

　　　　　　　　 x＝1

检验：x＝1时(x－1)(x+2)＝0，1不是原分式方程的解，原分式方程无解.

例1　　 解方程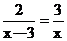

解：方程两边同乘x(x－3)，得

　　　　　　　 2x＝3x－9

解得　　　　　　 x＝9

检验：x＝9时 x(x－3)≠0，9是原分式方程的解.

例2　　 解方程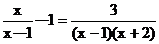

解：方程两边同乘(x－1)(x+2)，得