
请同学们回顾本节课所学的内容,有哪些收获?
师生活动:学生思考后,用自己语言归纳,教师适时点评,并关注以下几个问题:1、等边对等角;2、等腰三角形三线合一;3、等边三角形性质;4、等腰三角形常用辅助线作法(作底边上的高、作底边上的中线、作顶角的平分线)
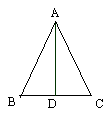 练习2:课本练习第2题(出示小黑板)
练习2:课本练习第2题(出示小黑板)
如图,在ABC中,AB=AC
(1)∵AD⊥BD,∴∠______ = ∠_____; ______ = ______(等腰三角形底边上的高与______、______重合)
(2)∵AD是中线 ∴_____ ⊥_____;∠_____= ∠_____(等腰三角形底边上的中线与_____、_____重合)
(3)∵AD是角平分线 ∴____ ⊥ ____;____= ____(等腰三角形顶角的平分线与______、_____重合)
6、 等边三角形各内角有什么关系?各等于多少度?
要求学生完成教师提出的问题,教师归纳:
(1)等腰三角形中顶角与底角的关系:顶角十 2 ×底角=180°
(2)推论:等边三角形三个内角相等,每一个内角都等于60°(板书)
教师与学生合作分析,口述(2)的证明过程。
活动4:提出问题:从性质1的证明过程可以知道,BD=CD,
∠ADB=∠ADC=90°,由此,你能得出等腰三角形还具有什么性质?
让学生运用数学语言表述所发现的规律,师生共同归纳得出:
性质2 等腰三角形的顶角的平分线垂直平分底边(板书)
即:等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合
三线合一(板书)
活动5:教师出示课本例1(小黑板显示)
例1 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,求∠DAE的度数
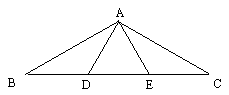
分析例1,剖析推理方法及依据,提出讨论问题,引导学生思考,根据学生回答教师板书例1过程,解略
5、 如果等腰三角形的一个内角是120°,则其它的两个角各是多少度?
4、 如果等腰三角形的一个角是40°,那么其它的两个角各是多少度?
3、如果等腰三角形的顶角是40°,那么它的底角的度数是多少?
2、 如果等腰三角形的底角等于40°,那么它的顶角的度数是多少?

 活动2:教师出示刚才剪下的等腰三角形纸片,标上字母如图所示:
活动2:教师出示刚才剪下的等腰三角形纸片,标上字母如图所示:
把边AB叠合到边AC上,这时点B与C重合,并出现折痕AD,观察图图形,△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
学生回答:△ADB与△ADC重合,∠B=∠C,∠BAD=∠CAD,∠ADB=∠CDA,BD=CD
活动3:由上面的性质我们可以得到等腰三角形如下性质:
性质1:等腰三角形的两个底角相等,简称:等边对等角(板书)
教师提问:这个命题的题设是什么?结论是什么?学生可结合图形回答
(板书)已知:在△ABC中,AB=AC
求证:∠B=∠C
说明:将等腰三角形写成已知时,通常写成“在△ABC中,AB=AC”而不写成“等腰”两个字
教师引等学生回答:要证两个角相等可以转化前面所学过的三角形全等,而图形只有一个三角形,如何添加辅助线使它转化为两个三角形?
通过刚才的折叠等腰三角形的实验,很容易得到辅助线,作高AD或作顶角的平分线AD,可由两位学生板演,教师巡视,并给订正。
同学们思考一下,还有没有其它辅助线的作法,教师可作提示:作中线AD,由学生口答,或者指导学生看课本证明。
教师归纳等腰三角形性质1,并指出它的几何符号语言的书写:
如上图:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
教师提出问题:练习1(口答)
1、 等腰直角三角形每一个锐角的度数是多少度?
活动1:请同学们把一张长方形的纸片对折,剪去(或用刀子裁)一个角,再把它展开,得到的是什么样三角形?
教师示范操作,然后学生跟着动手操作,观察得出结论:“剪刀剪过的两条边是相等的;剪出的图形是等腰三角形”,根据学生回答,板书:等腰三角形
师生共同回顾:有两条边相等的三角形,叫做等腰三角形,相等的两边叫做腰,另一条边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角
教师提问:剪出的三角形是轴对称图形吗?你能发现这个三角形有哪些特点吗?说一说你的猜想
学生思考并发表自已的看法,教师提出本节课所要解决的问题
师生归纳:等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴(板书)
教师说明:对称轴是一条直线,而三角形的中线是线段,因此不能说等腰三角形底边上的中线是它的对称轴。
16.3等腰三角形同步练习
第1题. 已知等腰三角形的一个内角为80°,则它的另两角为________________.
第2题. 在△ABC中, ∠ABC=∠C=2∠A,BD是∠ABC的平分线,DE∥BC,则图中等腰三角形的个数是( )
A.2 B.3 C.4 D.5
第3题. 如下图,△MNP中, ∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )

A.8+2a B.8+a C.6+a D.6+2a
第4题. O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为( )

A.8cm B.9cm C.10cm D.11cm
第5题. 已知:如下图,P,Q是△ABC边上BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
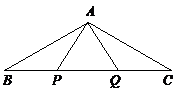
第6题. 等腰三角形底边中点与一腰的距离为6,则腰上的高为______.
第7题. 如下图,DE是线段BC垂直平分线上两点,连DB、DC、EB、EC,则∠DBC与∠DCB的关系是________,∠DBE与∠DCE的关系是________.

第8题. 等腰三角形底角的外角比顶角的外角大30°,则这个三角形各内角度数是________.
第9题. 等腰三角形有一个角是50°,那么其他两个角的度数是____________.
第10题. 如下图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=______.

第11题. △ABC是等腰三角形,D为BC上一点,DE∥AB且交AC于E,请判断△EDC是什么三角形?并说明理 由.
由.
第12题. 已知AE平分∠DAC,AE∥BC,那么AB=AC吗?请简要说明理由.

第13题. 等腰三角形的两边长为3和6,则这个三角形的周长为( )
A.9 B.12 C.15 D.12或15
 第14题. 如下图,PQ为Rt△MPN斜边上的高, ∠M=45°,则图中等腰三角形的个数是( )
第14题. 如下图,PQ为Rt△MPN斜边上的高, ∠M=45°,则图中等腰三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
第15题. 如下图,在△ABC中,AB=AC, ∠A=50°,P是△ABC内一点, ∠PCB=∠PCA,且∠PBC=∠PBA, 则∠BPC度数为( )
则∠BPC度数为( )
A.115° B.100° C.130° D.140°
第16题. 下列命题正确的个数是( )
①如果等腰三角形内一点到底边两端点的距离相等,那么过这点与顶点的直线必垂直于底边;②如果把等腰三角形的底边向两个方向延长相等的线段,那么延长线段的两个端点与顶点距离相等;③等腰三角形底边中线上一点到两腰的距离相等;④等腰三角形高上一点到底边的两端点距离相等.
A.1个 B.2个 C.3个 D.4个
第17题. 等腰三角形顶角是84°,则一腰上的高与底边所成的角的度数是( )
A.42° B.60° C. 36° D. 46°
第18题. 等边三角形两条角平分线所夹锐角的度数是( )
A.120° B. 150° C.60° D.90°
 第19题. 如下图,∠ABC中,AD⊥BC,AB=AC, ∠BAD=30°,且AD=AE,则∠EDC等于( )
第19题. 如下图,∠ABC中,AD⊥BC,AB=AC, ∠BAD=30°,且AD=AE,则∠EDC等于( )
A.10° B.12.5° C.15° D. 20°
第20题. 如下图,△ABC中,点D在AC上,且AB=AD, ∠ABC=∠C+30°,则∠CBD等于
 ( )
( )
A.15° B. 18° C. 20° D. 22.5°
第21题. 如果一个三角形的一条边上的中点到其他两边的距离相等,那么它一定是( )
A.等边三角形 B.等腰三角形
C.不等边三角形 D.不等腰钝角三角形
第22题. 如下图,在△ABC中,AB=AC, ∠A=36°,BD、CE分别是∠ABC、∠ACB的平分线,则图中等腰 三角形的个数为( )
三角形的个数为( )
A.12 B.10 C.9 D.8
第23题. 一个等腰三角形的一个内角为90°,那么这个等腰三角形的一个底角为( )
A.90° B. 45° C. 50° D. 22.5°
第24题. 等腰三角形的两条边长分别为15cm和7cm,则它的周长为( )
A.37cm B.29cm C.37cm或29cm D.无法确定
第25题. △ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠BAD∶∠CAB=1∶3,则∠B等于_______度.

第26题. 已知Rt△ABC是轴对称图形,且∠C=90°,那么∠B=_____度,∠A=______度;点A的对应点是______,点C的对应点是_______.
第27题. 在△ABC中,边AB、BC的垂直平分线相交于点P,则PA、PB、PC的大小关系是_________.
第28题. 如图,在△ABC中,AB=AC,D,E分别是BC边上的两点,且满足AD=AE=BD=CE,则图中与∠B相等的角有________个角,分别是________________________.
图中全等的三角形有___对,分别是 _____________________________
_____________________________
第29题. 已知:如下图,AB=AC,BD⊥AC,请探索∠DBC与∠A的关系并说 明理由.
明理由.
第30题. 已知线段a,b(a>2b),以a、b为边作等腰三角形,则( )
A.只能作以a为底边的等腰三角形
B.只能作以b为底边的等腰三角形
C.可以作分别以a、b为底的等腰三角形
D.不能作符合条件的等腰三角形
第31题. 如图,在△ABC中,BC=5 cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是___________ cm.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com