4．　 如图7，已知在△ABC中，∠ABC与∠ACB的平分线交于点O，若∠A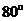＝，则∠BOC＝　　　

3．　 如图6，△ABC是等腰直角三角形，∠A＝，BD是角平分线，DE⊥BC，若BC＝10，则△DEC的周长为　　　　

2．　 如图5，在△ABC中，∠C＝，AD平分∠BAC交BC于D，若BC=20，BD︰CD=5︰3，则D到AB的距离DE是　　　

1．　 如图4，已知AB∥CD，OA平分∠BAC，OC平分∠AOD，OE⊥AC于点E，且OE=2，则两平行线间的距离为　　　　

5．　 与相交两直线距离相等的点在(　 )

A.　　 一条直线上

B.　　　 一条射线上

C.　　　 两条相互垂直的直线上

D.　　 两条相互垂直的射线上　　　　　　　　　　　　　　　　　　　　　　　　　　　

4．下列说法中，错误的是　　 (　 )

A.　　 三角形任意两个角的平分线的交点在三角形的内部

B.　　　 任意两个角的平分线的交点到三角形三个顶点的距离相等

C.　　　 三角形两个角的平分线的交点到三边的距离相等

D.　　 三角形两个角的平分线的交点在第三个角的平分线上

3．如图，L1.L2.L3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有(　 )

A.　 一处B.　 二处　　　　 C.　 三处　 D.四处

2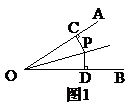．　 如图2，△ABC中，AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足，则下列四个结论：(1)AD上任意一点到点C、D的距离相等；(2)AD上任意一点到AB、AC的距离相等；(3)AD⊥BC且BD＝CD；(4)∠BDE=∠CDF,其中正确的个数是(　 )

A.　 1个　　 B.　 2个　　 C.　 3个　　 D.　 4个

1．　 如图1，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则下列结论中错误的是(　 )

A.　 PC=PD　　 B.OC=OD　　 C.∠CPO=∠DPO　　　　 D.OC=PC

课本练习第2题、习题16.3第1题

教学反思：

　　 本节课通过对等腰三角形叠合操作引出等腰三角形是轴对称图形，进而得到等腰三角形的性质1：等边对等角，这种操作有利于学生发现等腰三角形性质的证明，给出三种不同的辅助线，是用来培养学生的发散思维能力。新教材中例1设计与旧人教版求“人字形的角度”相比具有一定难度，为此，在讲完性质1后，设计如教案中练习1，一方面是用来巩固性质1，其中练习1中2、3、4具有变式教学思想，另一方面是为推论及性质2作准备。教案中练习2是用来巩固性质2，重点是培养学生的几何符号语言表达能力。让学生回顾，是为了培养学生的语言表达能力，同时加深学生对所学知识的理解，促进学生对学习过程的进行反思。在整个教学过程中，本人利用多种教学方法，使学生在实验中提出问题，解决问题的途径，而不知不觉地进入学习氛围，把学生从被动学习步入主动想学的习惯。总之，在本节教学中，我始终坚持以学生为主体，教师为主导，致力启用学生已掌握的知识，充分调动学生的兴趣和积极性，使他们最大限度地参与到课堂的活动中，在整个教学过程中我以启发学生，挖掘学生潜力，培养学生应用意识，提高学生学习数学素养。