
2.使学生理解分式通分的意义,掌握分式通分的方法及步骤.
教学重点:
让学生知道约分、通分的依据和作用,学会分式约分与通分的方法.
教学难点:
1.掌握分式的基本性质,掌握分式约分方法,熟练进行约分,并了解最简分式的意义.
P5习题17.1第1、2题,第3题(2)(4)
什么是分式?什么是有理式?
P5习题17.1第3题(1)(3)
例1 下列各有理式中,哪些是整式?哪些是分式?
(1) ; (2)
; (2)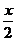 ; (3)
; (3) ; (4)
; (4) .
.
解:属于整式的有:(2)、(4);属于分式的有:(1)、(3).
注意:在分式中,分母的值不能是零.如果分母的值是零,则分式没有意义.例如,在分式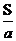 中,a≠0;在分式
中,a≠0;在分式 中,m≠n.
中,m≠n.
例2
当 取什么值时,下列分式有意义?
取什么值时,下列分式有意义?
(1) ; (2)
; (2) .
.
分析 要使分式有意义,必须且只须分母不等于零.
解 (1)分母 ≠0,即
≠0,即 ≠1.
≠1.
所以,当 ≠1时,分式
≠1时,分式 有意义.
有意义.
(2)分母2 ≠0,即
≠0,即 ≠-
≠-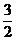 .
.
所以,当 ≠-
≠-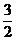 时,分式
时,分式 有意义.
有意义.
形如 (A、B是整式,且B中含有字母,B≠0)的式子,叫做分式.其中 A叫做分式的分子,B叫做分式的分母.
(A、B是整式,且B中含有字母,B≠0)的式子,叫做分式.其中 A叫做分式的分子,B叫做分式的分母.
整式和分式统称有理式, 即有 理式 整式,分式.
理式 整式,分式.
(1)面积为2平方米的长方形一边长3米,则它的另一边长为_____米;
(2)面积为S平方米的长方形一边长a米,则它的另一边长为________米;
(3)一箱苹果售价p元,总重m千克,箱重n千克,则每千克苹果的售价是___元;

概念 例
值为0:
分式 有(无)意义
作业:练习1.下列各式分别回答哪些是整式?哪些是分式?
 ,
,  , 2a-3b,
, 2a-3b,  ,
, 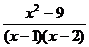 ,
,
练习2 分式  ,当y 时,分式有意义;当y 时,分式没有意义;当y 时,分式的值为0.
,当y 时,分式有意义;当y 时,分式没有意义;当y 时,分式的值为0.
练习3 讨论探索
当x取什么数时,分式 (1)有意义 (2)值为零?
(1)有意义 (2)值为零?
各抒已见.看谁说得最全.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com