
8.课后反思:
7.作业:
P5练习 1约分:第(2)(4)题,习题17.1第4题
6.小结:(1)请你分别用数学语言和文字表述分式的基本性质;
(2)分式的约分运算,用到了哪些知识?
让学生发表,互相补充,归结为:①因式分解;②分式基本性质;③分式中符号变换规律;约分的结果是,一般要求分、分母不含“-”.
(3)把几个异分母的分式,分别化成与原来分式相等的同分母的分式,叫做分式的通分.分式通分,是让原来分式的分子、分母同乘以一个适当的整式,根据分式基本性质,通分前后分式的值没有改变.通分的关键是确定几个分式的公分母,从而确定各分式的分子、分母要乘以什么样的“适当整式”,才能化成同一分母.确定公分母的方法,通常是取各分母所有因式的最高次幂的积做公分母,这样的公分母叫做最简公分母.
5.练习P5 练习 第2题:通分
4. 例4 通分
(1)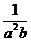 ,
,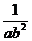 ; (2)
; (2)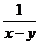 ,
,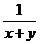 ; (3)
; (3)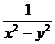 ,
,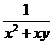
解 (1)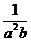 与
与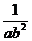 的最简公分母为a2b2,所以
的最简公分母为a2b2,所以
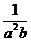 =
=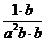 =
=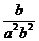 ,
,
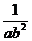 =
=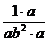 =
=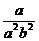 .
.
(2)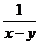 与
与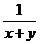 的最简公分母为(x-y)(x+y),即x2-y2,所以
的最简公分母为(x-y)(x+y),即x2-y2,所以
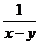 =
=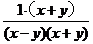 =
=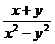 ,
, 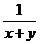 =
=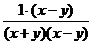 =
=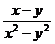 .
.
请同学们根据这两小题的解法,完成第(3)小题.
3.练习:P5 练习 第1题:约分(1)(3)
2. 例3 约分
(1)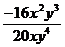 ; (2)
; (2)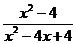
分析 分式的约分,即要求把分子与分母的公因式约去.为此,首先要找出分子与分母的公因式.
解(1)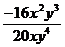 =-
=-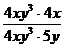 =-
=-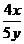 . (2)
. (2)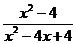 =
=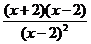 =
=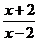 .
.
约分后,分子与分母不再有公因式. 分子与分母没有公因式称为最简分式.
1.分式的基本性质
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
用式子表示是:
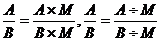 ( 其中M是不等于零的整式).
( 其中M是不等于零的整式).
与分数类似,根据分式的基本性质,可以对分式进行约分和通分.
2.几个分式最简公分母的确定.
教学过程:
1.分子、分母是多项式的分式约分;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com