
把几个异分母的分式,分别化成与原来分式相等的同分母的分式,叫做分式的通分.分式通分,是让原来分式的分子、分母同乘以一个适当的整式,根据分式基本性质,通分前后分式的值没有改变.通分的关键是确定几个分式的公分母,从而确定各分式的分子、分母要乘以什么样的“适当整式”,才能化成同一分母.确定公分母的方法,通常是取各分母所有因式的最高次幂的积做公分母,这样的公分母叫做最简公分母.
4.所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母.
(3)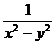 ,
,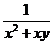 .
.
分析 :分式的通分,即要求把几个异分母的分式分别化为与原来的分式相等的同分母的分式.通分的关键是确定几个分式的公分母;要归纳出分式分式是多项式如何确定最简公分母,一般应先将各分母分解因式,然后按上述的方法确定分母.
练习
通分:
(1)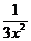 ,
,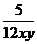 ;(2)
;(2)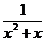 ,
,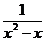 (3)
(3)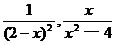 .
.
合作交流解法.
板演并互批.
3.相同字母(或因式)的幂取指数最大的;
2.各分式的分母中所有字母或因式都要取到;
6、例3 通分
(1)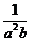 ,
,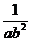 ; (2)
; (2)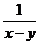 ,
,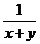 ;
;
答:1.取各分式的分母中系数最小公倍数;
5.练习:填空:
(1)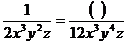 ; (2)
; (2)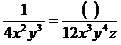 ;
;
(3)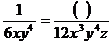 .
.
求下列各组分式的最简公分母:
(1)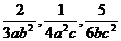 ; (2);
; (2);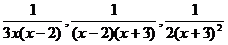
(3)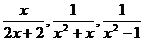
4.讨论: (1)求分式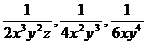 的(最简)公分母.
的(最简)公分母.
分析:对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x3,字母y为底的幂的因式,取其最高次幂y4,再取字母z.所以三个分式的公分母为12x3y4z.
(2) 求分式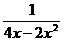 与
与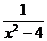 的最简公分母.
的最简公分母.
分析:先把这两个分式的分母中的多项式分解因式,即
4x-2x2= -2x(x-2),x2-4=(x+2)(x-2),
把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即2x(x+2)(x-2)就是这两个分式的最简公分母.
请同学概括求几个分式的最简公分母的步骤.
3.和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分.
通分的关键是确定几个分式的公分母.
2.)什么叫分数的通分? 先独立思考再交流总结变号法则.
注意转化为例1的类型.引导学生用多种方法解题.
(1) 赋值法(2)增值代入作商法
答:把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分.
2、分式的通分
(1).把分数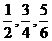 通分.
通分.
解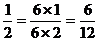 ,
,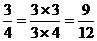 ,
,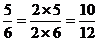
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com