
习题17。1 部分练习
3.反比例函数的图象在哪个象限由k决定,且y值随x值变化只能在“每一个象限内”研究.
 4.在y=
4.在y=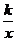 (k≠0)中,由于x≠0,同时y≠0,因此双曲线两个分支不可能到达坐标轴.
(k≠0)中,由于x≠0,同时y≠0,因此双曲线两个分支不可能到达坐标轴.
2.反比例函数的性质.
1.画反比例函数的图象.
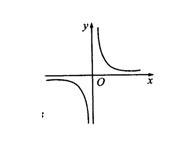
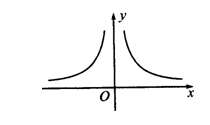
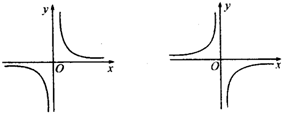
2.(2005年中考·宣昌)如图所示的函数图象的关系式可能是( )
A.y=x B.y=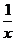 C.y=x2
D.y=
C.y=x2
D.y=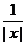
例题 指出当k>0时,下列图象中哪些可能是y=kx与y=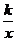 (k≠0)在同一坐标系中的图象 ( )
(k≠0)在同一坐标系中的图象 ( )
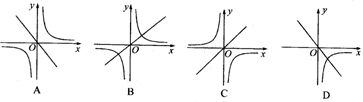
[分析] 对于y=kx来说,当k>0时,图象经过一、三象限,当k<0时,图象经过二、四象限;对于y=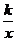 来说,当k>0时,图象在一、三象限,当k<0时,图象在二、四象限,所以应选B.
来说,当k>0时,图象在一、三象限,当k<0时,图象在二、四象限,所以应选B.
 [答案] B
[答案] B
备选例题
1.(2005年中考·泉州)请你写出一个反比例函数的解析式,使它的图象在第一、三象限.
2. 探究 反比例函数y=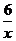 和y=-
和y=-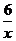 的图象有什么共同特征?它们之间有什么关系?
的图象有什么共同特征?它们之间有什么关系?
做一做 把y=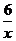 和y=-
和y=-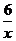 的图象放到同一坐标系中,观察一下,看它们是否对称.
的图象放到同一坐标系中,观察一下,看它们是否对称.
归纳 反比例函数y=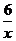 和y=-
和y=-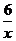 的图象的共同特征:
的图象的共同特征:
(1)它们都由两条曲线组成.
(2)随着x的不断增大(或减小),曲线越来越接近坐标轴(x轴、y轴).
(3)反比例函数的图象属于双曲线(hyperbola).
此外,y=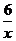 的图象和y=-
的图象和y=-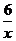 的图象关于x轴对称,也关于y轴对称.
的图象关于x轴对称,也关于y轴对称.
活动3
做一做 在平面直角坐标系中画出反比例函数y=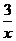 和y=-
和y=-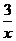 的图象.
的图象.
交流 两个函数图象都用描点法画出?
活动4
[分析] 由y=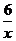 和y=-
和y=-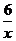 的图象及y=
的图象及y=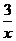 和y=-
和y=-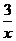 的图象知道,
的图象知道,
(1)它们有什么共同特征和不同点?
(2)每个函数的图象分别位于哪几个象限?
(3)在每一个象限内,y随x的变化而如何变化?
猜想 反比例函数y=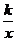 (k≠0)的图象在哪些象限由什么因素决定?在每一个象限内,y随x的变化情况如何?它可能与坐标轴相交吗?
(k≠0)的图象在哪些象限由什么因素决定?在每一个象限内,y随x的变化情况如何?它可能与坐标轴相交吗?
[归纳] (1)反比例函数y=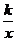 (k为常数,k≠0)的图象是双曲线.
(k为常数,k≠0)的图象是双曲线.
(2)当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小.
(3)当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大.
活动2
问题:我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,那么反比例函数y=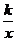 (k为常数且k≠0)的图象是什么样呢?
(k为常数且k≠0)的图象是什么样呢?
1. 尝试 用描点法来画出反比例函数的图象.
例2: 画出反比例函数y=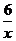 和y=-
和y=-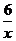 的图象.
的图象.
解:列表
|
x |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
y=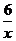 |
|
|
-1 |
|
-1.5 |
-2 |
|
-6 |
|
3 |
|
|
1 |
|
y=-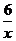 |
|
1 |
1.2 |
|
|
3 |
6 |
|
|
|
-1.5 |
|
|
|
(请把表中空白处填好)
描点,以表中各对应值为坐标,在直角坐标系中描出各点.
连线,用平滑的曲线把所描的点依次连接起来.
3.试用描点法画出下列函数的图象:(1)y=2x; (2)y=1-2x.
活动1
问题:1.若y=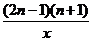 是反比例函数,则n必须满足条件 n≠
是反比例函数,则n必须满足条件 n≠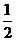 或n≠-1 .
或n≠-1 .
2.用描点法画图象的步骤简单地说是 列表 、 描点 、 连线 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com