3、探究新知

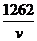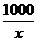(1)三个函数表达式：t＝、y＝、S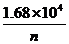＝有什么共同结构特征？你能用一个一般形式来表示吗？

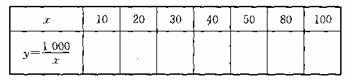(2)对于函数关系式y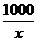＝，完成下表：

当x越来越大时．y怎样变化？这说明x与y具备怎样的关系?

(3)类比一次函数的概念给上述新的函数下一个恰当的定义．

2、提出问题

上面问题．1的第(3)题及问题2、3中，自变量与因变量分别是什么?三个问题的函数表达式分别是什么?这三个函数关系式可以叫正比例函数吗?可以叫一次函数吗?试与问题1中的(1)(2)比较．

1、新课引入

①京沪高速公路全长为1 262 km，现有一辆汽车沿京沪高速公路从上海驶往北京．

　　 回答下列问题：

　　 (1)若汽车每行驶100 km油耗为6．8 L，则汽车行驶了x km后的耗油量为Q L．请用含x的代数式表示Q，并指出题中的自变量、因变量及两个变量间的函数关系．

　　 (2)若这辆汽车驶离上海时油箱中有油150 L，则汽车行驶了x km后油箱的剩油量为P L，请用含有x的代数式表示P，并指出题中的自变量、因变量及两个变量之间的函数

关系．　　

(3)设汽车的速度是匀速的，速度为v km·h，该车从上海到北京所用时间为t h，你能用含v的代数式表示t吗?

②某住宅小区要种植一个面积为1 000 m²的矩形草坪，草坪的长为y(单位：m)，宽为x(单位：m)，用含x的式子表示y．

③已知北京市的总面积为1．68×10⁴km²，人均占有的土地面积S(单位：km²／人)随全市总人口n(单位：人)的变化而变化．请用含n的代数式表示S．

2．已知一次函数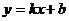的图像与反比例函数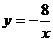的图像交于A、B两点，且点A的横坐标和点B的纵坐标都是－2 ，

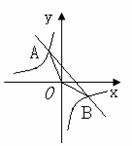求(1)一次函数的解析式；

　 (2)△AOB的面积

1．已知反比例函数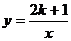的图象在每个象限内函数值y随自变量x的增大而减小，且k的值还满足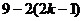≥2k－1，若k为整数，求反比例函数的解析式

2．已知点(－1，y₁)、(2，y₂)、(π，y₃)在双曲线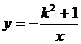上，则下列关系式正确的是(　　　 )

(A)y₁＞y₂＞y₃　　　　　　　　　　 (B)y₁＞y₃＞y₂　　

(C)y₂＞y₁＞y₃　　　　　　　　　　 (D)y₃＞y₁＞y₂

1．若直线y＝kx+b经过第一、二、四象限，则函数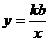的图象在(　　　 )

例3．见教材P51

分析：反比例函数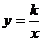的图象位置及y随x的变化情况取决于常数k的符号，因此要先求常数k，而题中已知图象经过点A(2，6)，即表明把A点坐标代入解析式成立，所以用待定系数法能求出k，这样解析式也就确定了.

例4．见教材P52

例1．(补充)若点A(－2，a)、B(－1，b)、C(3，c)在反比例函数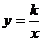(k＜0)图象上，则a、b、c的大小关系怎样？

分析：由k＜0可知，双曲线位于第二、四象限，且在每一象限内，y随x的增大而增大，因为A、B在第二象限，且－1＞－2，故b＞a＞0；又C在第四象限，则c＜0，所以

b＞a＞0＞c

说明：由于双曲线的两个分支在两个不同的象限内，因此函数y随x的增减性就不能连续的看，一定要强调“在每一象限内”，否则，笼统说k＜0时y随x的增大而增大，就会误认为3最大，则c最大，出现错误.

此题还可以画草图，比较a、b、c的大小，利用图象直观易懂，不易出错，应学会使用.

例2． (补充)如图，　 一次函数y＝kx+b的图象与反比例函数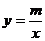的图象交于A(－2，1)、B(1，n)两点

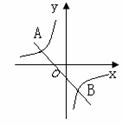(1)求反比例函数和一次函数的解析式

(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围

分析：因为A点在反比例函数的图象上，可先求出反比例函数的解析式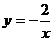，又B点在反比例函数的图象上，代入即可求出n的值，最后再由A、B两点坐标求出一次函数解析式y＝－x－1，第(2)问根据图象可得x的取值范围x＜－2或0＜x＜1，这是因为比较两个不同函数的值的大小时，就是看这两个函数图象哪个在上方，哪个在下方.

2．反比例函数的图象是什么？有什么性质？

复习上节课所学的内容

1．什么是反比例函数？