
5.函数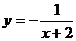 中自变量x的取值范围是
中自变量x的取值范围是
4.已知y与x成反比例,且当x=-2时,y=3,则y与x之间的函数关系式是 ,
当x=-3时,y=
3.矩形的面积为4,一条边的长为x,另一条边的长为y,则y与x的函数解析式为
2.若函数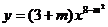 是反比例函数,则m的取值是
是反比例函数,则m的取值是
1.苹果每千克x元,花10元钱可买y千克的苹果,则y与x之间的函数关系式为
例1.见教材P47
分析:因为y是x的反比例函数,所以先设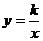 ,再把x=2和y=6代入上式求出常数k,即利用了待定系数法确定函数解析式.
,再把x=2和y=6代入上式求出常数k,即利用了待定系数法确定函数解析式.
例1.(补充)下列等式中,哪些是反比例函数
(1)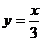 (2)
(2)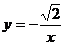 (3)xy=21 (4)
(3)xy=21 (4)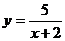 (5)
(5)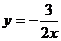
(6)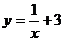 (7)y=x-4
(7)y=x-4
分析:根据反比例函数的定义,关键看上面各式能否改写成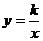 (k为常数,k≠0)的形式,这里(1)、(7)是整式,(4)的分母不是只单独含x,(6)改写后是
(k为常数,k≠0)的形式,这里(1)、(7)是整式,(4)的分母不是只单独含x,(6)改写后是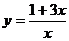 ,分子不是常数,只有(2)、(3)、(5)能写成定义的形式
,分子不是常数,只有(2)、(3)、(5)能写成定义的形式
例2.(补充)当m取什么值时,函数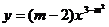 是反比例函数?
是反比例函数?
分析:反比例函数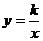 (k≠0)的另一种表达式是
(k≠0)的另一种表达式是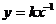 (k≠0),后一种写法中x的次数是-1,因此m的取值必须满足两个条件,即m-2≠0且3-m2=-1,特别注意不要遗漏k≠0这一条件,也要防止出现3-m2=1的错误.
(k≠0),后一种写法中x的次数是-1,因此m的取值必须满足两个条件,即m-2≠0且3-m2=-1,特别注意不要遗漏k≠0这一条件,也要防止出现3-m2=1的错误.
解得m=-2
例3.(补充)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5
(1) 求y与x的函数关系式
(2) 当x=-2时,求函数y的值
分析:此题函数y是由y1和y2两个函数组成的,要用待定系数法来解答,先根据题意分别设出y1、 y2与x的函数关系式,再代入数值,通过解方程或方程组求出比例系数的值.这里要注意y1与x和y2与x的函数关系中的比例系数不一定相同,故不能都设为k,要用不同的字母表示.
略解:设y1=k1x(k1≠0),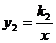 (k2≠0),则
(k2≠0),则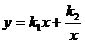 ,代入数值求得k1=2,
,代入数值求得k1=2,
k2=2,则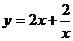 ,当x=-2时,y=-5
,当x=-2时,y=-5
2.体育课上,老师测试了百米赛跑,那么,时间与平均速度的关系是怎样的?
1.回忆一下什么是正比例函数、一次函数?它们的一般形式是怎样的?
教材第46页的思考题是为引入反比例函数的概念而设置的,目的是让学生从实际问题出发,探索其中的数量关系和变化规律,通过观察、讨论、归纳,最后得出反比例函数的概念,体会函数的模型思想.
教材第47页的例1是一道用待定系数法求反比例函数解析式的题,此题的目的一是要加深学生对反比例函数概念的理解,掌握求函数解析式的方法;二是让学生进一步体会函数所蕴含的“变化与对应”的思想,特别是函数与自变量之间的单值对应关系.
补充例1、例2都是常见的题型,能帮助学生更好地理解反比例函数的概念.补充例3是一道综合题,此题是用待定系数法确定由两个函数组合而成的新的函数关系式,有一定难度,但能提高学生分析、解决问题的能力.
3.难点的突破方法:
(1)在引入反比例函数的概念时,可适当复习一下第11章的正比例函数、一次函数等相关知识,这样以旧带新,相互对比,能加深对反比例函数概念的理解
(2)注意引导学生对反比例函数概念的理解,看形式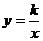 ,等号左边是函数y,等号右边是一个分式,自变量x在分母上,且x的指数是1,分子是不为0的常数k;看自变量x的取值范围,由于x在分母上,故取x≠0的一切实数;看函数y的取值范围,因为k≠0,且x≠0,所以函数值y也不可能为0.讲解时可对照正比例函数y=kx(k≠0),比较二者解析式的相同点和不同点.
,等号左边是函数y,等号右边是一个分式,自变量x在分母上,且x的指数是1,分子是不为0的常数k;看自变量x的取值范围,由于x在分母上,故取x≠0的一切实数;看函数y的取值范围,因为k≠0,且x≠0,所以函数值y也不可能为0.讲解时可对照正比例函数y=kx(k≠0),比较二者解析式的相同点和不同点.
(3)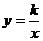 (k≠0)还可以写成
(k≠0)还可以写成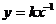 (k≠0)或xy=k(k≠0)的形式
(k≠0)或xy=k(k≠0)的形式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com