1．会用描点法画反比例函数的图象

8. 作业设计

(1)课本第46页习题17．1第3，8题．

(2)课本第61页复习课17第10题．

7. 小结

　 说说你在本节课的收获．

6. 巩固练习

(1)课本第49页练习．

(2)课本第50页练习第l，2题．

5. 讨论交流

(1)反比例函数的图象

　 可以是如右图所示的曲线吗?　 为什么?

(2)函数研究的是两个变量之间的关系，对于反比例函数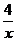y＝及y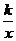＝ (k为正整数)，当自变量x的值增加时，函数y是如何变化的?与同组同学交流一下，你是如何得出这个结论的?

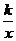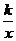(3)反比例函数y＝，与y＝－，(k为正整数)的图象有什么共同特征?它们之间有什么关系?能否根据y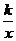＝的图象，画出y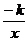＝的图象?

4. 探究新知　　

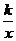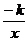画出反比例函数y＝，与y＝，(k为正整数)的图象．

说明：(1)k的值由学生自己取某个正整数．(如1，2，3…)

(2)两个图象画在同一坐标系中，用铅笔画出y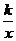＝的图象，用红笔画出y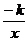＝的图象．

　 思考：

　(1)从以上作图，你发现反比例函数图象是什么?

(图象由两条曲线组成，我们说反比例函数y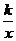＝ (k为正整数)的图象是双曲线)

　(2) y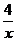＝的图象是双曲线，双曲线的两分支分别在第几象限? y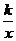＝ (k为正整数)的图象，它们在第几象限?

　(3)从上面我们发现y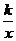＝ (k为正整数)的图象是双曲线，双曲线的两分支分别在第一、三象限，你能从其他角度说明理由吗?

　(4)观察反比例函数(k为常数，k≠0)的图象，你得出哪些结论？与你的同学讲行交流．

3. 众说画图

　　 在以上作图中，你有哪些收获，说给其他同学听听．

答：(1)列表时x不可以取0．

(2)自变量的值可以选取一些互为相反数的值，这样做既简化计算，又便于对称性描点．

(3)多取一些值、多描一些点，画出的函数图象会更准确．

(4)连线时：按自变量从小到大的顺序依次用光滑的曲线连接．

2. 提出问题

　 试一试，画出反比例函数y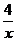＝，的图象．

1. 新课引入

(1)根据上节课的学习，说说你对反比例函数的认识．

(2)对于一次函数y=kx+b (k≠0)的性质，我们是如何研究的?(根据定义，先研究一次函数图象的画法，再利用图象研究一次函数的性质)

(3)对于反比例函数y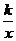＝，(k≠0，k为常数)，下一步我们应研究什么?(反比例函数的图象)

(4)你还记得作函数图象的一般步骤吗?

　　 (在自变量的取值范围内取一些值，列表、描点、连线)

已知函数y＝y₁+y₂，y₁与x+1成正比例，y₂与x成反比例，且当x＝1时，y＝0；当x＝4时，y＝9，求当x＝－1时y的值

答案：y＝4