
1、一个矩形的面积为20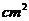 ,相邻的两条边长分别为Xcm, Ycm,那么变量Y是变量X的函数吗?是反比例函数吗?为什么?
,相邻的两条边长分别为Xcm, Ycm,那么变量Y是变量X的函数吗?是反比例函数吗?为什么?
2.(1)下列函数中,反比例函数是 .
A.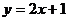 B.
B.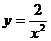 C.
C.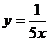 D.
D.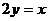
(2)已知:(x1,y1)和(x2,y2)是双曲线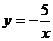 上两点,当x1<x2<0时,y1与y2
上两点,当x1<x2<0时,y1与y2
的大小关系是 .
A.y1=y2 B.y1<y2 C.y1>y2 D.y1与y2的大小关系不确定
(3)若函数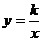 的图象过点(3,-7),那么它一定还经过点
.
的图象过点(3,-7),那么它一定还经过点
.
A.(3,7) B.(-3,-7) C.(-3,7) D.(2,-7)
(4)若反比例函数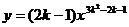 的图象位于第二、四象限,则k的值是
.
的图象位于第二、四象限,则k的值是
.
A.0 B.0或1 C.0或2 D.4
学法指要
[例] 如图代13-4-1,在等腰梯形ABCD中,CD∥AB,CD=6,AD=10,∠A=60°,以
CD为弦的弓形弧与AD相切于D,P是AB上一动点,可以与B重合但不与A重合,DP交弓形弧于Q.
反比例函数
教学目标:
(1)从现实情境和学生已有的知识经验出发,讨论两个变量之间的相互关系,加深对函数概念的理解。
(2)经历抽象反比例函数概念的进程,领会反比例函数的意义,理解反比例函数的概念。
(3) 学会从数学角度理解和抽象问题,建立模型,运用所学反比例函数的概念,判断哪些关系是反比例函数关系,并解决实际问题,发展学生的应用意识。
重点、难点
经历抽象反比例函数概念的过程,领会反比例函数的意义,理解反比例函数的概念及求表达式。
教学过程
师:请看大屏幕:
屏幕显示问题:京沪高速公路是我国第一条国道主干线,全长约为1262km,汽车沿京沪高速公路从上海驶往北京
(1)若汽车每小时行驶85千米, 那么汽车行驶2小时的路程是多少?4小时呢?10小时呢? t小时呢?
(2)汽车行驶的路程s(km)与时间t(h)之间有什么关系?变量s是t的函数吗?若是,那么它是什么函数?若不是,请说明理由。
生:170千米、340千米、850千米、85t千米。 S=85t,当给定一个t的值,相应就确定一个s的值,因此s是t的函数。并且是正比例函数。
师:请看大屏幕:
屏幕显示问题:电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)请你用含有R的代数式表示I;(2)利用你写出的关系式完成下表:
|
R/Ω |
20 |
40 |
60 |
80 |
100 |
|
I/A |
|
|
|
|
|
当R越来越大时,I是怎样变化的?当R越来越小呢?
(3)变量I是R的函数吗?为什么?
生:I=220/R
当电阻R越来越大时,电流I越来越小;当R越来越小时,I越来越大,当给定一个R的值,相应的就确定一个I值,因此I是R的函数。
师:请看大屏幕:
屏幕显示问题: 请设计一个面积为6平方米的矩形花园。
矩形的两边可以任意取吗?应该满足什么条件?
生:(有多种不同设计方案),应满足矩形的乘以宽等于6。
师:观察上面两个函数表达式,是否具有共同的特点?
生:自变量与因变量的乘积不变。
师:能否举出类似的实际例子?
生:(踊跃发言)
师:同学们举的例子也都具有自变量与因变量的乘积不变的特点,你能否用一个一般的函数表达式来描述这一特点?
生: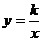 或xy=k
或xy=k
师:一般地,如果两个变量x,y之间的关系可以表示成: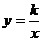 (k为常数,K≠0)的形式,那么称y是x的反比例函数。其中自变量不能为0。另外,
(k为常数,K≠0)的形式,那么称y是x的反比例函数。其中自变量不能为0。另外,
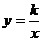 和xy=k是反比例函数的两种不同形式的表达式,这两种表达式是等价的。两个变量之间的关系式只要满足其中一种表达形式,便可以根据概念判断其是反比例函数。
和xy=k是反比例函数的两种不同形式的表达式,这两种表达式是等价的。两个变量之间的关系式只要满足其中一种表达形式,便可以根据概念判断其是反比例函数。
师: 请看大屏幕:
屏幕显示问题:在下列函数表达式中,x均为自变量,哪些是反比例函数?每一个反比例函数相应的k值是多少?
(1) 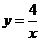 , (2)
, (2) 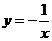 , (3)xy=10, (4)
, (3)xy=10, (4) 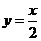
生: (1)(2)(3)是反比例函数,它们的k值分别是4,-1,10。
师:下面,我们来看一些实际实际问题,请同学们根据条件写出函数表达式,并判断是否为反比例函数。
思维基础
知识是思维的基础,通过下述练习,要掌握下述基础知识.
1.(1)函数 叫做反比例函数;它的图象是 .
(2)反比例函数的性质:①当k>0,图象的两个分支分别在 象限,在每一
个象限内y随x的增大而 ,②k<0,图象的两个分支分别在 象限,在每一个象限内,y随x的增大而 .
(3)k为何值时,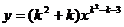 是反比例函数,即k=
.
是反比例函数,即k=
.
(4)反比例函数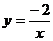 图象在
象限.
图象在
象限.
从生活中的实例,引出反比例函数的概念:函数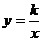 (k是常数,k≠0)叫做反比
(k是常数,k≠0)叫做反比
例函数.在具体教学中,要采取与正比例函数对照的方法,用描点法画出反比例函数图象,结合图象,引导学生归纳出反比例函数的性质,进而介绍用待定系数法求反比例函数解析式的方法,在教学中,比较法和待定系数法要贯穿教学的始终.
反比例函数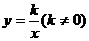 可写成另一种形式:
可写成另一种形式: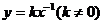 .自变量x的指数显然
.自变量x的指数显然
是正比例函数的相反数,通过对照,一定分清反比例函数的图象是双曲线,但在具体事物或特定条件下,画出的图象可能是双曲线的一部分,这取决于自变量的取值范围(例如x>0,它只有一个分支在第一象限……).所以在画图象前,一定要弄清自变量的取值范围.
3.
已知反比例函数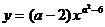 ,当
,当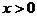 时,y随x的增大而增大,
时,y随x的增大而增大,
求函数关系式
答案:3.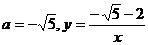
2.反比例函数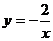 ,当x=-2时,y=
;当x<-2时;y的取值范围是 ;
,当x=-2时,y=
;当x<-2时;y的取值范围是 ;
当x>-2时;y的取值范围是
1.若函数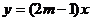 与
与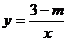 的图象交于第一、三象限,则m的取值范围是
的图象交于第一、三象限,则m的取值范围是
3.在平面直角坐标系内,过反比例函数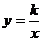 (k>0)的图象上的一点分别作x轴、y轴的垂线段,与x轴、y轴所围成的矩形面积是6,则函数解析式为
(k>0)的图象上的一点分别作x轴、y轴的垂线段,与x轴、y轴所围成的矩形面积是6,则函数解析式为
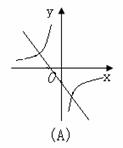
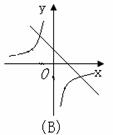
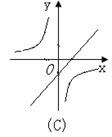
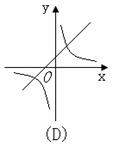
2.函数y=-ax+a与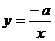 (a≠0)在同一坐标系中的图象可能是( )
(a≠0)在同一坐标系中的图象可能是( )
1.已知反比例函数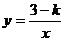 ,分别根据下列条件求出字母k的取值范围
,分别根据下列条件求出字母k的取值范围
(1)函数图象位于第一、三象限
(2)在第二象限内,y随x的增大而增大
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com