2、提出问题

投影出在物理中学过的杠杆定律：阻力×阻力臂＝动力×动力臂．

问题：

(1)当阻力和阻力臂分别是1 200牛和O.5米时，动力F和动力臂l有何关系?

(2)力臂为l.5米时，撬动石头至少要用多大的力?

(3)当想使动力F不超过(2)中所用力的一半时，你如何处理?

1、引入新课

前面几堂课我们学习了反比例函数在生活中的一些运用，今天我们主要学习如何用反比例函数解决科学中的一些问题．　　

5. 作业设计①必做题：　　 (1)课本第61页第2题．

(2)某打印店要完成一批电脑打字任务，每天完成75页，需8天，设每天完成的页数y，所需天数x．问y与x是何种函数关系? 若要求在5天内完成任务，每天至少要完成几页?

4. 小结　 让学生以小组为单位进行合作交流，总结出本节课的收获与困惑，而后师生共同得出结论：(1)学习了反比例函数的应用．(2)确定反比例函数时，先根据题意求出走，而后根据已有知识得出反比例函数．(3)求“至少”“最多”值时，可根据函数的性质得到．

3. 巩固练习

例2某蓄水池的排水管道每小时排水8 m³，6 h可将满池水全部排空． (1)蓄水池的容积是多少? (2)如果增加排水管，使每时的排水量达到Q(m³)，将满池水排空所需时间为t(h)，求Q与t之间的函数关系式． (3)如果准备在5 h内将满池水排空，那么每小时排水量至少为多少? (4)已知排水管的最大排水量为每时12 m³，那么最少多长时间可将满池水全部排空?

这个巩固练习前三问与例题类似，设置第四问是为了与第一堂课相衔接，使学生学会将函数关系式变形．授课时，教师要对第四问进行细致分析．由学生板书，师生分析，为小结作准备．

2. 提出问题、解决问题

(1)审完题后，你的切入点是什么?，

由题意知：船上载物重是30×8=240吨，这是一个不变量，也就是在这个卸货过程中的常量，所以根据卸货速度×卸货天数=货物重量，可以得到v与t的函数关系即vt=240，

v=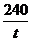，所以v是t的反比例函数，且t>0．

(2)你们再回忆一下，今天求出的反比例函数与昨天求出的反比例函数在思路上有什么不同?(昨天求出的反比例函数，常数k是直接知道的，今天要先确定常数k)

(3)明确了问题的区别，那么第二问怎样解决?

根据反比例函数v=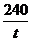 (t>0)，当t=5时，v=48．即每天至少要48吨．这样做的答

案是不错的，这里请同学们再仔细看一下第二问，你有什么想法．实际上这里是不等式关系，5日内完成，可以这样化简t=240／v，0<t≤5，即0<240／v≤5，可以知道v≥48即至少要每天48吨．但是课本把第二问中“至少”处理成等式，使问题简单了．

1. 引入新课

　　 上节课我们学习了实际问题与反比例函数，使我们认识到了反比例函数在现实生活中的实际存在．今天我们将继续学习这一部分内容，请看例1(投影出课本第50页例2)．

例1码头工人以每天30吨的速度往一艘轮船上装载货物，把轮船装载完毕恰好用了8天时间．轮船到达目的地后开始卸货，卸货速度v(吨／天)与卸货时间t(天)之间有怎样的关系? 由于紧急情况，船上货物必须在不超过5日内卸载完毕，那么每天至少卸货多少吨?

7. 作业

①必做题：

　　 (1)课本第61页练习第1题．

　　 (2)一场暴雨过后，一洼地存雨水20 m³，如果将雨水全部排空需t分钟，每分钟排水量为a m³，且排水时间在5-10分钟之间：

　　 a你能把t表示成a的函数吗?

　　 b当每分钟排水量3 m³时，排水量时间多少分钟?

　　 c当排水时间4．5分钟时，每分钟排水量多少m³ ？(保留一位小数)

②选做题：

　(1)某食品集团有限公司现存20 kg含盐30%的盐水，现要蒸发掉部分水分，如果蒸发掉x kg水分后的盐水浓度为y，你能写出y与x的函数关系式吗?

　(2)一定质量的CO₂放在容器中，当它体积为V=5 m³时，它的密度p=1．98 kg／m³．

　　 a当把这些CO₂放人5．5 m³的容器时，密度是多少?

　　 b当密度为1．06 kg／m³时，它的容积是多少?

6. 小结

　 请同学们发表一下自己的看法，说说对本课的感受．

　 师生共同小结：

(1)反比例函数图象是两支曲线，要么在一、三象限；要么在二、四象限．

(2)今天我们学习的是反比例函数在实际中的运用，d＝10 000／s还需加上条件s>0，也就是只有第一象限内有一支曲线．

　 (3)把一个实际问题转化为数学问题求值，体现了数学应用价值．

5. 巩固练习

　　 以小组为单位讨论解决问题，而后各小组由发言代表讲述．