
2.完成某项任务可获得500元报酬,考虑由x人完成这项任务,试写出人均报酬y(元)与人数x(人)之间的函数关系式
1.京沈高速公路全长658km,汽车沿京沈高速公路从沈阳驶往北京,则汽车行完全程所需时间t(h)与行驶的平均速度v(km/h)之间的函数关系式为
例1.见教材第57页
分析:(1)问首先要弄清此题中各数量间的关系,容积为104,底面积是S,深度为d,满足基本公式:圆柱的体积 =底面积×高,由题意知S是函数,d是自变量,改写后所得的函数关系式是反比例函数的形式,(2)问实际上是已知函数S的值,求自变量d的取值,(3)问则是与(2)相反
例2.见教材第58页
分析:此题类似应用题中的“工程问题”,关系式为工作总量=工作速度×工作时间,由于题目中货物总量是不变的,两个变量分别是速度v和时间t,因此具有反比关系,(2)问涉及了反比例函数的增减性,即当自变量t取最大值时,函数值v取最小值是多少?
 例1.(补充)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图像如图所示(千帕是一种压强单位)
例1.(补充)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图像如图所示(千帕是一种压强单位)
(1)写出这个函数的解析式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
分析:题中已知变量P与V是反比例函数关系,并且图象经过点A,利用待定系数法可以求出P与V的解析式,得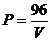 ,(3)问中当P大于144千帕时,气球会爆炸,即当P不超过144千帕时,是安全范围.根据反比例函数的图象和性质,P随V的增大而减小,可先求出气压P=144千帕时所对应的气体体积,再分析出最后结果是不小于
,(3)问中当P大于144千帕时,气球会爆炸,即当P不超过144千帕时,是安全范围.根据反比例函数的图象和性质,P随V的增大而减小,可先求出气压P=144千帕时所对应的气体体积,再分析出最后结果是不小于 立方米
立方米
寒假到了,小明正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小明立即告诉同伴分散趴在冰面上,匍匐离开了危险区.你能解释一下小明这样做的道理吗?
教材第57页的例1,数量关系比较简单,学生根据基本公式很容易写出函数关系式,此题实际上是利用了反比例函数的定义,同时也是要让学生学会分析问题的方法.
教材第58页的例2是一道利用反比例函数的定义和性质来解决的实际问题,此题的实际背景较例1稍复杂些,目的是为了提高学生将实际问题抽象成数学问题的能力,掌握用函数观点去分析和解决问题的思路.
补充例题一是为了巩固反比例函数的有关知识,二是为了提高学生从图象中读取信息的能力,掌握数形结合的思想方法,以便更好地解决实际问题
3.难点的突破方法:
用函数观点解实际问题,一要搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式(包括已学过的基本公式),这一步很重要;二是要分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围;三要熟练掌握反比例函数的意义、图象和性质,特别是图象,要做到数形结合,这样有利于分析和解决问题.教学中要让学生领会这一解决实际问题的基本思路.
2.难点:分析实际问题中的数量关系,正确写出函数解析式
1.重点:利用反比例函数的知识分析、解决实际问题
2.渗透数形结合思想,提高学生用函数观点解决问题的能力
1.利用反比例函数的知识分析、解决实际问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com