
活动2
[例3]小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米,
(1) 动力F与动力臂l有怎样的函数关系式?当动力臂为1。5米时,撬动石头至少需要多大的力?
(2) 若想使动力F不超过题(1)中所用力的一半,遇动力臂至少要加长多少?
师生行为:先由学生根据 “杠杆定律”解决上述问题。教师可引导学生揭示“杠杆平衡”与“反比例函数”之间的关系。教师在此活动中应重点关注:
① 学生能否主动用“杠杆定律”中杠杆定律中杠杆平衡的条件去理解实际问题,从而建立与反比例函数的关系;
② 学生能否面对困难,认真思考,寻找解题的途径;
③ 学生能否积极主动地参与数学活动,对数学和物理有着浓厚的兴趣。
分析:“撬动石头”就意味着达到了“杠杆平衡”,因此可用“杠杆定律”来解决此问题。
解:(1)根据 “杠杆定律”有
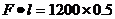 。得
。得 。
。
当l=1.5时,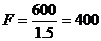 .
.
因此,撬动石头至少需要400牛顿的力。
(3) 若想使动力F不超过题(1)中所用的一半,即不超过200牛,根据“杠杆定律”有
F·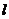 =600,
=600,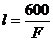 。
。
当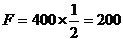 时,
时,
3-1.5=1.5(米)
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米。
想想还有哪些方法可以解决这个问题?
思考:用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长越省力?
总结:其实反比例函数在实际运用中非常广泛。例如在解决经济预算中的应用。
活动3
问题:某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55-0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x-0.4)元成反比例。又当x=0.65时,y=0.8。
(1) 求y与x之间的函数关系式;
(2) 若每度电的成本价0.3元,电价调至0.6元时,请你预算一下本年度电力部门的纯收入是多少?
师生行为:由学生先独立思考,然后小组内讨论完成。教师应给以“学困生”一定的帮助。
解:(1)∵y与x成反比例,
∴设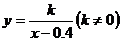 .
.
把x=0.65,y=0.8。代入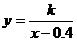 ,得
,得
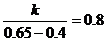
解得k=0.2
∴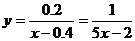 。
。
∴y与x之间的函数关系为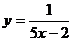
(2)根据题意,本年度电力部门的纯收入为
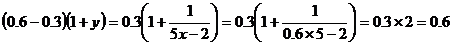 (亿元)
(亿元)
答:本年度的纯收入为0.6亿元。
师生共析:(1)由题目提供的信息知y与x之间是反比例函数关系,把x-0.4看成一个变量,于是可设出表达式,再由题目的条件x=0.65时,y=0.8得出字母系数的值;
(2)纯收入=总收入-总成本。
2. 教师应给“学困生” 一点物理学知识的引导.
分析:从题目中提供的信息看变量I与R之间的反比例函数关系,可设出其表达式,再由已知条件(I与R的一对对应值)得到字母系数k的值。
解:设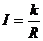 ∵R=5,I=2,于是
∵R=5,I=2,于是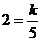 ,所以k=10,∴
,所以k=10,∴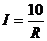
(2)当I=0.5时,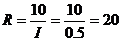 (欧姆)
(欧姆)
“给我一支点,我可以把地球撬动.”这是哪一位科学家的名言?这里瘟涵着什么样的原理呢?这是古希腊科学家阿基米得的名言。公元前3世纪,古希腊科学家阿基米得发现了著名的“杠杆定律”:若两物体与支点的距离反比与其重量,则杠杆平衡,通俗一点可以描述为
阻力×阻力臂=动力×动力臂
下面我们就来看一例子。
1. 可由学生独立思考,领会反比例函数在物理学中的综合应用.
活动
问题:在物理学中,有很多量之间的变化是反比例函数的关系,因此,我们可以借助于反比例函数的图象和性质解决一些物理学中的问题,这也称为跨学科应用.下面的例子就是其中之一。
1. 在某一电路中,保持电压不变,电流I和电阻R成反比例,当电阻R=5欧姆时,电流I=2I.
(1) 求I与R之间的函数关系式;
(2) 当电流I=0.5时,求电阻R的值.
师生行为
一场暴雨过后,一洼地存雨水20米3,如果将雨水全部排完需t分钟,排水量为a米3/分,且排水时间为5-10分钟
(1)试写出t与a的函数关系式,并指出a的取值范围;
(2)请画出函数图象
(3)根据图象回答:当排水量为3米3/分时,排水的时间需要多长?
3.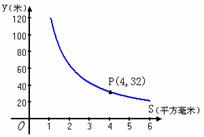 你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识,一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示:
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识,一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示:
(1)写出y与S的函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少米?
2.已知甲、乙两地相s(千米),汽车从甲地匀速行驶到达乙地,如果汽车每小时耗油量为a(升),那么从甲地到乙地汽车的总耗油量y(升)与汽车的行驶速度v(千米/时)的函数图象大致是( )
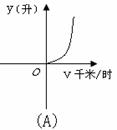
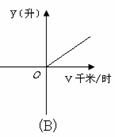
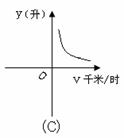
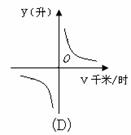
1.某厂现有800吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
(A)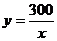 (x>0)
(B)
(x>0)
(B)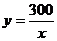 (x≥0)
(x≥0)
(C)y=300x(x≥0) (D)y=300x(x>0)
例3.见教材第58页
分析:题中已知阻力与阻力臂不变,即阻力与阻力臂的积为定值,由“杠杆定律”知变量动力与动力臂成反比关系,写出函数关系式,得到函数动力F是自变量动力臂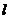 的反比例函数,当
的反比例函数,当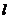 =1.5时,代入解析式中求F的值;(2)问要利用反比例函数的性质,
=1.5时,代入解析式中求F的值;(2)问要利用反比例函数的性质,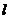 越大F越小,先求出当F=200时,其相应的
越大F越小,先求出当F=200时,其相应的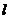 值的大小,从而得出结果.
值的大小,从而得出结果.
例4.见教材第59页
分析:根据物理公式PR=U2,当电压U一定时,输出功率P是电阻R的反比例函数,则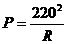 ,(2)问中是已知自变量R的取值范围,即110≤R≤220,求函数P的取值范围,根据反比例函数的性质,电阻越大则功率越小,
,(2)问中是已知自变量R的取值范围,即110≤R≤220,求函数P的取值范围,根据反比例函数的性质,电阻越大则功率越小,
得220≤P≤440
例1.(补充)为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范为 ;
药物燃烧后,y关于x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过______分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
分析:(1)药物燃烧时,由图象可知函数y是x的正比例函数,设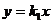 ,将点(8,6)代人解析式,求得
,将点(8,6)代人解析式,求得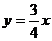 ,自变量0<x≤8;药物燃烧后,由图象看出y是x的反比例函数,设
,自变量0<x≤8;药物燃烧后,由图象看出y是x的反比例函数,设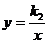 ,用待定系数法求得
,用待定系数法求得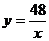
(2)燃烧时,药含量逐渐增加,燃烧后,药含量逐渐减少,因此,只能在燃烧后的某一时间进入办公室,先将药含量y=1.6代入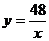 ,求出x=30,根据反比例函数的图象与性质知药含量y随时间x的增大而减小,求得时间至少要30分钟
,求出x=30,根据反比例函数的图象与性质知药含量y随时间x的增大而减小,求得时间至少要30分钟
(3)药物燃烧过程中,药含量逐渐增加,当y=3时,代入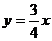 中,得x=4,即当药物燃烧4分钟时,药含量达到3毫克;药物燃烧后,药含量由最高6毫克逐渐减少,其间还能达到3毫克,所以当y=3时,代入
中,得x=4,即当药物燃烧4分钟时,药含量达到3毫克;药物燃烧后,药含量由最高6毫克逐渐减少,其间还能达到3毫克,所以当y=3时,代入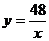 ,得x=16,持续时间为16-4=12>10,因此消毒有效
,得x=16,持续时间为16-4=12>10,因此消毒有效
2.台灯的亮度、电风扇的转速都可以调节,你能说出其中的道理吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com