3. 总结一下怎样进行分式的加减法？

概括

同分母的分式相加减，分母不变，把分子相加减；

异分母的分式相加减，先通分，变为同分母的分式，然后再加减.

2. 试一试：

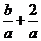计算：(1)；(2)　　　　　　　　　　　　　　　　　　　　

1. 回忆：同分母的分数的加减法法则：

同分母的分数相加减，分母不变，把分子相加减.

　　　　　　 分式的乘方

　　　　　 分式的乘除法　　　 约分　　 例

分式运算

　　　　　　　　　 　　　 同分母

　　　　　 分式的加减法　　　　　　　

　　　　　　 　　　　　　　 异分母　　　 通分

5. 将得到的结果化成最简分式(整式).

作业：课本2、3、4.

4. 公分母保持积的形式，将各分子展开.

3. 用公分母通分后，进行同分母分式的加减运算.

2. 准确地得出各分式的分子、分母应乘的因式.

　　 异分母分式的加减法步骤：

1. 正确地找出各分式的最简公分母.

求最简公分母概括为：(1)取各分母系数的最小公倍数；(2)凡出现的字母为底的幂的因式都要取；(3)相同字母的幂的因式取指数最大的.取这些因式的积就是最简公分母.

6.练习：计算

(1)　　　　　　　 (2)

(3)(4)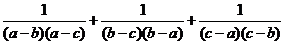　　 复习分数的加减法法则类比引出异分母分式的加减法法则