
§17.3 可化为一元一次方程的分式方程(2)
教学目标:
1、进一步熟练地解可化为一元一次方程的分式方程.
P14 习题17.3第1题(1)(2)、第2题
⑴、什么是分式方程?举例说明;
⑵、解分式方程的一般步骤:在方程的两边都乘以最简公分母,约去分母,化为整式方程.解这个整式方程..验根,即把整式方程的根代入最简公分母,看结果是不是零,若结果不是0,说明此根是原方程的根;若结果是0,说明此根是原方程的增根,必须舍去.
⑶、解分式方程为什么要进行验根?怎样进行验根?
2. 例2 解方程: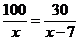 .
.
解 方程两边同乘以x(x-7),约去分母,得
100(x-7)=30x.
解这个整式方程,得
x=10.
检验:把x=10代入x(x-7),得
10×(10-7)≠0
所以,x=10是原方程的解.
1. 例1 解方程: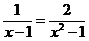 .
.
解 方程两边同乘以(x2-1),约去分母,得
x+1=2.
解这个整式方程,得
x=1.
解到这儿,我们能不能说x=1就是原分式方程的解(或根)呢?细心的同学可能会发现,当x=1时,原分式方程左边和右边的分母(x-1)与(x2-1)都是0,方程中出现的两个分式都没有意义,因此,x=1不是原分式方程的解,应当舍去.所以原分式方程无解.
我们看到,在将分式方程变形为整式方程时,方程两边同乘以一个含未知数的整式,并约去了分母,有时可能产生不适合原分式方程的解(或根),这种根通常称为增根.因此,在解分式方程时必须进行检验.
轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.
分 析
设轮船在静水中的速度为x千米/时,根据题意,得
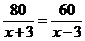 . (1)
. (1)
概 括
方程(1)中含有分式,并且分母中含有未知数,像这样的方程叫做分式方程.
思 考
怎样解分式方程呢?有没有办法可以去掉分式方程中的分母把它转化为整式方程呢?试动手解一解方程(1).
方程(1)可以解答如下:
方程两边同乘以(x+3)(x-3),约去分母,得
80(x-3)=60(x+3).
解这个整式方程,得
x=21.
所以轮船在静水中的速度为21千米/时.
概 括
上述解分式方程的过程,实质上是将方程的两边乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.
列分式方程解应用题的一般步骤:
(1)审清题意;
(2)设未知数(要有单位); 例
(3)根据题目中的数量关系
列出式子,找出相等关
系,列出方程;
(4)解方程,并验根,还要看
方程的解是否符合题意;
(5)写出答案(要有单位).
本课小结:列分式方程与列一元一次方程解应用题的差别是什么?
你能总结一下列分式方程应用题的步骤吗? 各抒己见畅所欲言
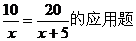 各抒己见畅所欲言说心里话.
各抒己见畅所欲言说心里话.
解析:设大车的速度为2x千米/时,小车的速度为5x千米/时,根据题意得
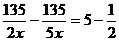 解之得x=9
解之得x=9
经检验x=9是原方程的解
当x=9时,2x=18,5x=45
答:大车的速度为18千米/时,小车的速度为45千米/时
练习:(1)甲乙两人同时从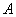 地出发,骑自行车到
地出发,骑自行车到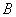 地,已知
地,已知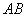 两地的距离为
两地的距离为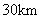 ,甲每小时比乙多走
,甲每小时比乙多走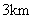 ,并且比乙先到40分钟.设乙每小时走
,并且比乙先到40分钟.设乙每小时走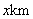 ,则可列方程为( )
,则可列方程为( )
A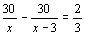 B.
B.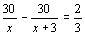 C.
C.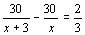 D.
D.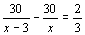
(2)我军某部由驻地到距离30千米的地方去执行任务,由于情况发生了变化,急行军速度必需是原计划的1.5倍,才能按要求提前2小时到达,求急行军的速度. 读题、审题、设元、找相等关系列方程
板演.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com