
小结与作业
1. 同底数幂的除法公式am÷an=am-n (a≠0,m>n)当m=n时,am÷an = 当m < n 时,am÷an =
例1计算:
(1)810÷810; (2)10-2; (3)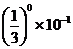
练 习:计算:
(1)(-0.1)0;(2)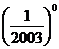 ;(3)2-2;(4)
;(3)2-2;(4)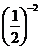 .
.
例2计算:
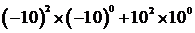 ;
; 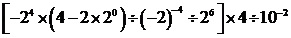
练习:计算
(1)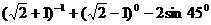
(2)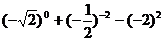
(3)(03苏州)计算:16÷(-2)3-(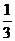 )-1+(
)-1+(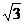 -1)0
-1)0
例3用小数表示下列各数:
(1)10-4; (2)2.1×10-5.
练习:用小数表示下列各数:
(1)-10-3×(-2) (2)(8×105)÷(-2×104)3
负指数幂 我们再来考察被除数的指数小于除数的指数的情况,
例如考察下列算式:
52÷55, 103÷107,
一方面,如果仿照同底数幂的除法公式来计算,得
52÷55=52-5=5-3, 103÷107=103-7=10-4.
另一方面,我们可利用约分,直接算出这两个式子的结果为
52÷55=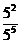 =
=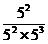 =
=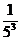 自主探究,合作交流思想:任何不等于零的数的-n (n为正整数)次幂,等于这个数的n 次幂的倒数.
自主探究,合作交流思想:任何不等于零的数的-n (n为正整数)次幂,等于这个数的n 次幂的倒数.
103÷107=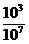 =
=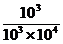 =
=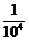
概 括:由此启发,我们规定: 5-3=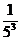 , 10-4=
, 10-4=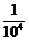 .
.
一般地,我们规定: 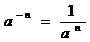 (a≠0,n是正整数)
(a≠0,n是正整数)
这就是说,任何不等于零的数的-n (n为正整数)次幂,等于这个数的n 次幂的倒数.
不等于零的零次幂的意义 先考察被除数的指数等于除数的指数的情况.例如考察下列算式:
52÷52,103÷103,a5÷a5(a≠0).
一方面,如果仿照同底数幂的除法公式来计算,得
52÷52=52-2=50,
103÷103=103-3=100,
a5÷a5=a5-5=a0(a≠0).
另一方面,由于这几个式子的被除式等于除式,由除法的意义可知,所得的商都等于1.
[概 括]
我们规定:
50=1,100=1,a0=1(a≠0).
这就是说:任何不等于零的数的零次幂都等于1.
自主探究,合作交流思想:任何不等于零的数的零次幂都等于1.
问题1 在§13.1中介绍同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢? 设置矛盾冲突,激发探究热情.
26、观察下列各式:
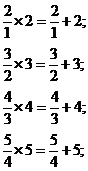
……
设n表示正整数,请你用含有n的等式表示这一规律.
25、(4分)(1)据统计,全球每分钟约有8500000 t污水排入江河湖海,这个排污量用科学记数法表示应为多少?
(2)自从扫描隧道显微镜发明后,世界上便诞生了一门新学科,这就是“纳米技术”.已知52个纳米长为0.000000052 m,用科学记数法表示此数为多少米?
24、若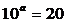 ,
, 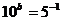 求
求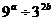 的值. (4分)
的值. (4分)
23、已知a、b互为相反数,c、d互为倒数,m的绝对值为2,求 的值.(4分)
的值.(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com