
4. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
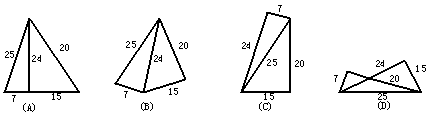
A B C D
3.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( )
A.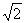 B.
B.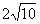 C.
C. D.以上都不对
D.以上都不对
2.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶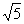
C.三边之比为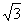 ∶2∶
∶2∶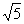 D. 三个内角比为1∶2∶3
D. 三个内角比为1∶2∶3
1.下列各组数据中,不能作为直角三角形三边长的是( )
A.9,12,15 B.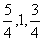 C.0.2,0.3,0.4 D.40,41,9
C.0.2,0.3,0.4 D.40,41,9
教科书第179页,习题第2题。
勾股定理有着悠久的历史,古巴比伦人和中国人看出了这个关系,古希腊毕达哥拉斯学派首先验证了这个关系。同学们,你们对勾股定理感兴趣吗?你想尝试自己验证勾股定理吗?请发挥你的才智,去探索勾股定理、去研究勾股定理吧!
2.你学到了哪些数学方法和数学思想?
(给出学生两个问题,让学生充分讨论、交流,得出结论,最后教师小结本课题。)
1.从两节课的课题学习中你有哪些收获?
2.教师可以利用课件介绍一些国外的勾股定理验证方法,重点介绍意大利文艺复兴时代著名画家达·芬奇对勾股定理的验证方法。
步骤:
(1)在一张长方形的纸板上画两个边长分别为a、b的正方形,并连结BC、FE。
(2)沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ。
(3)将纸板Ⅱ翻转后与Ⅰ拼成其它的图形。
(4)比较两个多边形ABCDEF和 的面积,你能验证勾股定理吗?(给学生充足的时间,进行独立思考,鼓励学生交流合作,教师巡视帮助,引导学习困难的学生。最后,验证方法让学生进行讲解、板演、叙述,教师做简单的总结。)
的面积,你能验证勾股定理吗?(给学生充足的时间,进行独立思考,鼓励学生交流合作,教师巡视帮助,引导学习困难的学生。最后,验证方法让学生进行讲解、板演、叙述,教师做简单的总结。)
你还想了解其他的验证方法吗?
1.利用五巧板拼“青朱出入图”(教师利用课件介绍“青朱出入图”的历史)。你能利用“青朱出入图”验证勾股定理吗?(给学生提供充分实践、探索和交流的时间,鼓励他们积极思考解决问题的方法,并与他人进行合作与交流。)
回顾上节课所学习的勾股定理的验证方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com