1．在直角三角形中，若已知任意两边，就可以运用勾股定理求出第三边．无直角时，可作垂线构造直角三角形.

18.1　勾股定理(2)

　知识领航

2、四个直角边分别为a、b斜边为c的直角三角形 一个腰长为c的等腰直角三角形

教学过程：

　　　　 (活动1)2002在北京召开的第24届国际数学家大会，这就是本届大会的会徽的图案(图1)

　　　　　　　　　　　　 (图1)

你见过这个图案吗？

　 　你知道它叫什么图？

　 　你听说过“勾股定理”吗？

这就是著名的“赵爽弦图” ，“赵爽弦图”既标志着中国古代数学成就，又像一只转动着的风车，欢迎着来自世界各地的数学家们。

板书(勾股定理)

活动2　 实验操作，探求新知

　(1) 相传2500年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系。(如图2)

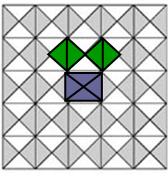
　　　　　　　　　　　　　　　　　　 (图2)

若用正方形的边长即等腰三角形的边来表示以上面积,你能发现等腰直角三角形三边之间有什么关系?

　 (2)等腰直角三角形是特殊的三角形,一般的三角形是否也有这样的特点?

　做一做　 观察图3三个正方形之间围成了一个什么样的三角形?

　　　　 你能计算出图中A、B、C的面积吗？

　 　　　如何计算C的面积？

　　　　　　 图3

3)请将结果填入下表，你能发现正方形A、B、C的面积关系吗？

　 即S_A+S_B=S_C

即直角边上的正方形的面积和等于斜边上的正方形的面积

　若直角三角形的直角边长为a、b，斜边c你能表示正方形的面积吗？

议一议:

　　　　 　　　　　　　　　　　b

　　　　　　　 　　　　　　　　　　c

　　　　　　　　　　　　　　　　 a

　　　　　　　　　　　　　　　 (图4)

根据上述等式,两直角边的平方和等于斜边的平方.

　　 如图4

　 a²+b²=c²

　活动3 是不是所有的 直角三角形都有这样的特点呢？ 折旧需要我们对一个一般直角三角形进行证明。

　　　 操作(一)

　　　 将课前准备的直角三角形拿出来，你能将四个直角三角形拼成以斜边c长为边长的正方形吗？小组活动。　 　　请两组同学上来比一比看那组快？

　　 设计意图：涉及拼图大部分同学都乐于参与包括学困生

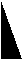
　　　　　　　　　 c

　 　　　　　　　b

　　　　　　　　 a

你能用两种不同的方法表示大正方形的面积吗？(设计意图：学困生至少能表示其中的一种)

　 (1)c²

　 (2)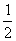abⅹ4+(a-b)²

　对比两种方法你能得到以上命题的结论吗？

操作(二)

这个正是著名的美国第十二总统加菲尔德的证明方法。

(讲述加菲尔德的故事，让学生了解历史，了解科学，学习他的聪明才智和探索精神)

通过以上证明我们得到该命题是正确的 ，它就是勾股定理，我们又称之为“商高定理”。在西方又称为“毕达哥拉斯定理”，“百牛定理”等

在汗代数学著作《周脾算经》记着商高的一段话意思是说：“把一直尺折段组成一个指直角三角形，若勾为三，股为四，弦为五”勾指的是较短的直角边，股是较长的直角边，弦是斜边。

　　　　　　　 弦

　　　　　　　　　　　 股　 　

　　　　　　　 勾

勾股定理的内容(板书)

　　 勾股定理的变形： c=

　　　　　　　　　　 a=

　　　　　　　　　　 b=

　用一用

　例1 (1)∠C=90⁰ 　a=2　 b=4求c

　　　 (·)若b=，c=3求a

　　 练习　 课本P27　 1、

　 是否有一种特殊的直角三角形已知一边也能求出另外的两边呢？

　　 例2　 ∠ A=30⁰　 ∠C=90^0， 　BC =1　 求AB AC； 求AB：AC：BC(3)若BC=k(k大于0)则(2)问题的结果是？

　　 　练习　 等腰直角三角形∠C=90^0， ，AC=AB=1

　　　　 求AB：AC：BC　

　　　 若腰的长度变化时，三边的比例会发生改变吗？

小结

勾股定理是一个古老而又应用广泛的定理，它以其简单、优美的形式，丰富、深刻的内容，充分反映了自然界的和谐关系。我国著名数学家华罗庚在谈论到“一旦人类遇到了外星人，该怎样与他们交谈”时，曾建议用一幅反映勾股定理的数形关系图来作为与外星人交谈的语言。这充分说明了勾股定理是自然界最本质最基本的规律之一。而在对于这样一个重要规律的发现和应用上，中国人走到了前面！

课外作业

　　　 已知　 ∠C=90^0，　CD⊥AB，BC=8　 AC=6 求斜边上的高

2、 用拼图方法证明勾股定理

教学重点:　 证明、探索、运用勾股定理

教学准备：　 1、学生准备　　 有关勾股定理的材料)

10．一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的验证方法.如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a,BC=b,AC=c，请利用四边形BCC′D′的面积验证勾股定理：a²+b²=c².

9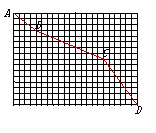．蚂蚁沿图中的折线从A点爬到D点，一共爬了多少厘米？(小方格的边长为1厘米)

拓广创新

u　　　　 试一试，你一定能成功哟！

7．如图，小李准备建一个蔬菜大棚，棚宽4m，高3m，长20m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请计算阳光透过的最大面积.

6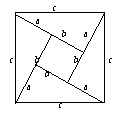．利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．观察图形，验证：c²＝a²+b²_.

5．如图,三个正方形中的两个的面积S₁＝25，S₂＝144，则另一个的面积S₃为________．　　　　　　　 　　　

综合运用

u　　　　 认真解答，一定要细心哟！