
启东市双鹤学校个人备课教案
|
P77~78/1~5 |
|
教师活动 |
学生活动 |
|
|
一、课堂引入 目前世界上许多科学家正在试图寻找其他星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等。我国数学家华罗庚曾建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的。这个事实可以说明勾股定理的重大意义。尤其是在两千年前,是非常了不起的成就。 以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。 |
让学生画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出AB的长。 |
|
|
教师活动 |
学生活动 |
|
|
你是否发现32+42与52的关系,52+122和132的关系,即32+42=52,52+122=132,那么就有勾2+股2=弦2。 对于任意的直角三角形也有这个性质吗? 二、例题讲解 例1(补充)已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。 求证:a2+b2=c2。 分析: ⑵拼成如图所示,其等量关系为:4S△+S小正=S大正 4× 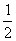 ab+(b-a)2=c2,化简可证。 ab+(b-a)2=c2,化简可证。⑶发挥学生的想象能力拼出不同的图形,进行证明。 ⑷ 勾股定理的证明方法,达300余种。这个古老的精彩的证法,出自我国古代无名数学家之手。激发学生的民族自豪感,和爱国情怀。 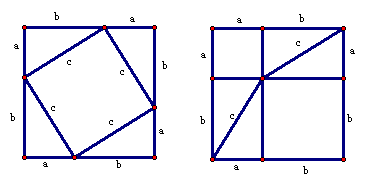 例2已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。 例2已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。 分析:左右两边的正方形边长相等,则两个正方形的面积相等。左边S=4× 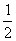 ab+c2,右边S=(a+b)2,左边和右边面积相等,即4× ab+c2,右边S=(a+b)2,左边和右边面积相等,即4×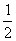 ab+c2=(a+b)2 ab+c2=(a+b)2 |
再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长。 让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明。 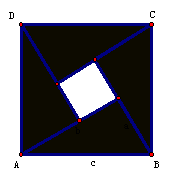 |
|
|
教师活动 |
学生活动 |
|
三、课堂练习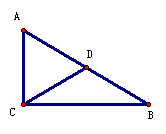 1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示) 1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)⑴两锐角之间的关系: ; ⑵若D为斜边中点,则斜边中线 ; ⑶若∠B=30°,则∠B的对边和斜边: ; ⑷三边之间的关系: 。 2.△ABC的三边a、b、c,若满足b2= a2+c2,则 =90°; 若满足b2>c2+a2,则∠B是 角; 若满足b2<c2+a2,则∠B是 角。 4.根据如图所示,利用面积法证明勾股定理。 |
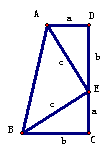 |
|
|
课 堂 总 结 |
1.勾股定理的内容 2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则 ⑴c= 。(已知a、b,求c) ⑵a= 。(已知b、c,求a) ⑶b= 。(已知a、c,求b) |
|
7.略 8.7.5尺 9.分三种情况讨论,最短距离是5cm 10.(1)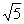 ,
, ;(2)
;(2)
1.C
2.B 3.12cm 4.49 5.12 6.依次填
18.1 勾股定理(3)
10.已知:正方形的边长为1.(1)如图(a),可以计算出正方形的对角线长为 .如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,
.如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,
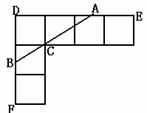 过C作直线交DE于A,交DF于B.若DB=
过C作直线交DE于A,交DF于B.若DB=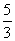 ,求DA的长度.
,求DA的长度.

9. 已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?
已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?
 拓广创新
拓广创新
u 试一试,你一定能成功哟!
8.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com