
18.1 勾股定理(3)
知识领航
1.在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=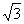 ,AB= 。 ,AB= 。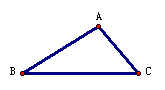 2.在Rt△ABC中,∠C=90°,S△ABC=30,c=13,且a<b,则a= ,b= 。 2.在Rt△ABC中,∠C=90°,S△ABC=30,c=13,且a<b,则a= ,b= 。3.已知:如图,在△ABC中,∠B=30°,∠C=45°AC= 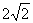 , ,求(1)AB的长;(2)S△ABC。 4.在数轴上画出表示- 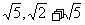 的点。 的点。 |
|
教师活动 |
学生活动 |
|
|
一、课堂引入 复习勾股定理的内容。本节课探究勾股定理的综合应用。 二、例习题分析 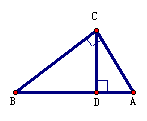 例1(补充)1.已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD= 例1(补充)1.已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=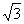 ,求线段AB的长。 ,求线段AB的长。 |
学生能够自己画图,并正确标图。学生分析:欲求AB,可由AB=BD+CD,分别在两个三角形中利用勾股定理和特殊角,求出BD=3和AD=1。或欲求AB,可由 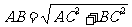 ,分别在两个三角形中利用勾股定理和特殊角,求出AC=2和BC=6。 ,分别在两个三角形中利用勾股定理和特殊角,求出AC=2和BC=6。 |
|
|
教师活动 |
学生活动 |
|
|
分析:本题是“双垂图”的计算题,“双垂图”是中考重要的考点,所以要求学生对图形及性质掌握非常熟练,能够灵活应用。目前“双垂图”需要掌握的知识点有:3个直角三角形,三个勾股定理及推导式BC2-BD2=AC2-AD2,两对相等锐角,四对互余角,及30°或45°特殊角的特殊性质等。 例2(补充)已知:如图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么? 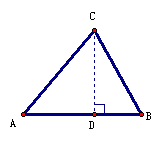 分析:由于本题中的△ABC不是直角三角形,所以根据题设只能直接求得∠ACB=75°。 小结:可见解一般三角形的问题常常通过作高转化为直角三角形的问题。并指出如何作辅助线? 例3(补充)已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。 分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。教学中要逐层展示给学生。 解:延长AD、BC交于E。 ∵∠A=∠60°,∠B=90°,∴∠E=30°。 ∴AE=2AB=8,CE=2CD=4, ∴BE2=AE2-AB2=82-42=48,BE= 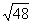 = =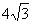 。 。 ∵DE2= CE2-CD2=42-22=12,∴DE= 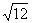 = =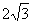 。 。∴S四边形ABCD=S△ABE-S△CDE= 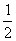 AB·BE- AB·BE-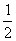 CD·DE= CD·DE=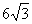 |
学生充分思考和讨论后,发现添置AB边上的高这条辅助线,就可以求得AD,CD,BD,AB,BC及S△ABC。 学生充分讨论还可以作其它辅助线吗?为什么? 学生深入体会 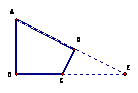 |
|
|
教师活动 |
学生活动 |
|
|
小结:不规则图形的面积,可转化为特殊图形求解,本题通过将图形转化为直角三角形的方法,把四边形面积转化为三角形面积之差。 例4(教材P76页探究3) 分析:利用尺规作图和勾股定理画出数轴上的无理数点,进一步体会数轴上的点与实数一一对应的理论。 变式训练:在数轴上画出表示 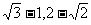 的点 的点 |
|
|
|
课 堂 总 结 |
1.“双垂图”需要掌握的知识点有:3个直角三角形,三个勾股定理及推导式BC2-BD2=AC2-AD2,两对相等锐角,四对互余角,及30°或45°特殊角的特殊性质等。 2.解一般三角形的问题常常通过作高转化为直角三角形的问题。清楚作辅助线不能破坏已知角。 |
|
|
P79/10、11、12 |
|
教师活动 |
学生活动 |
|
|
一、课堂引入 勾股定理在实际的生产生活当中有着广泛的应用。勾股定理的发现和使用解决了许多生活中的问题,今天我们就来运用勾股定理解决一些问题,你可以吗?试一试。 二、例习题分析 例1(教材P74页探究1)  分析:⑴在实际问题向数学问题的转化过程中,注意勾股定理的使用条件,即门框为长方形,四个角都是直角。⑶指出薄木板在数学问题中忽略厚度,只记长度,探讨以何种方式通过?⑷转化为勾股定理的计算,采用多种方法。⑸注意给学生小结深化数学建模思想,激发数学兴趣。 分析:⑴在实际问题向数学问题的转化过程中,注意勾股定理的使用条件,即门框为长方形,四个角都是直角。⑶指出薄木板在数学问题中忽略厚度,只记长度,探讨以何种方式通过?⑷转化为勾股定理的计算,采用多种方法。⑸注意给学生小结深化数学建模思想,激发数学兴趣。 |
⑵让学生深入探讨图中有几个直角三角形?图中标字母的线段哪条最长? |
|
|
教师活动 |
学生活动 |
|
|
例2(教材P75页探究2) 分析:⑴在△AOB中,已知AB=3,AO=2.5,利用勾股定理计算OB。 ⑵ 在△COD中,已知CD=3,CO=2,利用勾股定理计算OD则BD=OD-OB,通过计算可知BD≠AC。 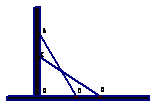 三、课堂练习 1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。 2.如图,山坡上两株树木之间的坡面距离是4 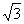 米,则这两株树之间的垂直距离是 米,水平距离是
米。 米,则这两株树之间的垂直距离是 米,水平距离是
米。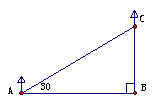 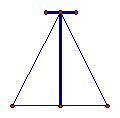 2题图 2题图
3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。 4.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少? |
⑶进一步让学生探究AC和BD的关系,给AC不同的值,计算BD。 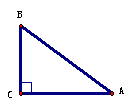 |
|
|
教师活动 |
学生活动 |
|
|
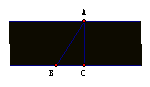
1.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米, ∠B=60°,则江面的宽度为 。 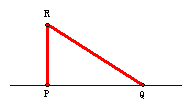 2.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。 2.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。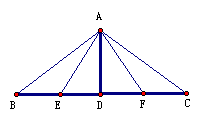 3.如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。 3.如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。(精确到1米) |
 |
|
|
课 堂 总 结 |
1.明确如何将实际问题转化为数学问题,注意条件的转化;学会如何利用数学知识、思想、方法解决实际问题。 2.进一步熟练使用勾股定理,探究直角三角形三边的关系:保证一边不变,其它两边的变化。 |
|
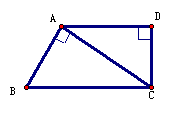 1.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, 1.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。 2.78~79/7、8、9 |
|
教师活动 |
学生活动 |
|
|
一、课堂引入 复习勾股定理的文字叙述;勾股定理的符号语言及变形。学习勾股定理重在应用。 二、、例习题分析 例1(补充)在Rt△ABC,∠C=90° ⑴已知a=b=5,求c。 ⑵已知a=1,c=2, 求b。 ⑶已知c=17,b=8, 求a。 ⑷已知a:b=1:2,c=5, 求a。 ⑸已知b=15,∠A=30°,求a,c。 分析:⑴已知两直角边,求斜边直接用勾股定理。⑵⑶已知斜边和一直角边,求另一直角边,用勾股定理的便形式。⑷⑸已知一边和两边比,求未知边。通过前三题让学生明确在直角三角形中,已知任意两边都可以求出第三边。后两题让学生 |
学生画好图形,并标好图形,理清边之间的关系。 |
|
|
教师活动 |
学生活动 |
|
|
明确已知一边和两边关系,也可以求出未知边,学会见比设参的数学方法,体会由角转化为边的关系的转化思想。 例2(补充)已知直角三角形的两边长分别为5和12,求第三边。 分析:已知两边中较大边12可能是直角边,也可能是斜边,因此应分两种情况分别进形计算。让学生知道考虑问题要全面,体会分类讨论思想。 例3(补充)已知:如图,等边△ABC的边长是6cm。 ⑴求等边△ABC的高。 ⑵求S△ABC。 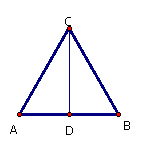 分析:勾股定理的使用范围是在直角三角形中,因此注意要创造直角三角形,作高是常用的创造直角三角形的辅助线做 法。欲求高CD,可将其置身于Rt△ADC或Rt△BDC中, 但只有一边已知,根据等腰三角形三线合一性质,可求AD=CD= 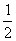 AB=3cm,则此题可解。 AB=3cm,则此题可解。三、课堂练习 1.填空题 ⑴在Rt△ABC,∠C=90°,a=8,b=15,则c= 。 ⑵在Rt△ABC,∠B=90°,a=3,b=4,则c= 。 ⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a= ,b= 。 ⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。 ⑸已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。 |
小组讨论,合作求解 |
|
|
教师活动 |
学生活动 |
|
 ⑹已知等边三角形的边长为2cm,则它的高为 ,面积为
。 ⑹已知等边三角形的边长为2cm,则它的高为 ,面积为
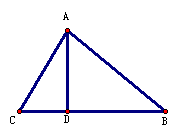
。2.已知:如图,在△ABC中,∠C=60°,AB= 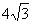 ,AC=4,AD是BC边上的高,求BC的长。 ,AC=4,AD是BC边上的高,求BC的长。
3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。 |
|
|
|
课 堂 总 结 |
1.明确在直角三角形中,已知任意两边都可以求出第三边,学会利用不同的条件转化为已知两边求第三边。 2.注意所给条件的不确定性,知道考虑问题要全面,体会分类讨论思想。 3.勾股定理的使用范围是在直角三角形中,因此注意要创造直角三角形,作高是常用的创造直角三角形的辅助线做法。 |
|
|
课 题 |
18.1勾股定理(二) |
课型 |
新授课 |
||||
|
教 学 目 标 |
知识与技能 |
1.会用勾股定理进行简单的计算。 2.树立数形结合的思想、分类讨论思想。 |
|||||
|
过程与方法 |
通过学生画好图形,标好图形,理清边边之间的关系,明确在直角三角形中,已知任意两边都可以求出第三边,学会利用不同的条件转化为已知两边求第三边。 |
||||||
|
情感目标 |
注意所给条件的不确定性,知道考虑问题要全面,体会分类讨论思想。 |
||||||
|
教学重点与难点 |
1.重点:勾股定理的简单计算。 2.难点:勾股定理的灵活运用。 |
||||||
|
教学资源 |
小黑板 |
||||||
|
预习作业 |
内容 |
完成自主练习与检测页的基础平台 |
|||||
|
时间 |
15分钟 |
方法 |
自学。 |
||||
|
要求 |
会应用勾股定理解决预习作业 |
||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com