4．　 如图18-11是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，如图18-12是以c为直角边的等腰直角三角形，请你开动脑筋，将它们拼成能证明勾股定理的图形。

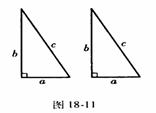
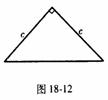
(1)　　　 画出拼成的这个图形的示意图，它是什么图形？

(2)　　　 用(1)中的图形证明勾股定理。假设图18-11的直角三角形若干个，你能拼出另一种能证明勾股定理的图形吗？请画出示意图。(不必证明)

反思提炼

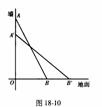
3．　 如图18-10，一根长10米的木棒斜靠在墙上，木棒的顶端距地面的垂直距离AO=8米。

(1)　　　 若木棒的顶端下滑2米，请你猜一猜，木棒的底端是否右滑2米？为什么？

(2)　　　 若木棒的顶端下滑3米，请你猜一猜，木棒的底端是否右滑3米？为什么？

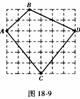
2．　 如图18-9是由边长为100米的小正方形网格组成的绿色草地，小明在上面沿实线走一周，它走的路程是多少米？(用无理数表示即可)

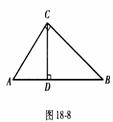
1．　 如图18-8，在Rt△ABC中，∠C=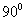，AB=13，AC=5，CD⊥AB于D，你能求出BD的长吗？请试一试。

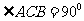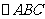4．如图18-7，，以的三边为边在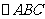旁边作三个正方形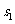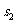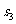，、、分别表示这三个正方形的面积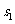，=81、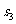=225，则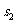的值为多少？

创新演练

3．已知等边三角形的周长为18，则它的面积为___________.

2．你能在数轴上作出表示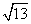的点吗？请试一试。

1．若直角三角形的三边长分别为2，4，x，则x的可能值有　 (　　 )

　 A、1个　　　 B、2个　　　　 C、3个　　　 D、4个

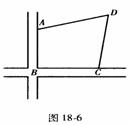
3．　 农民王伯伯承包了一块四边形水稻田ABCD，如图18-6，他量得AB=90m,BC=120m,CD=130m,AD=140m,且B点正好位于两条互相垂直的马路的拐角处，请你帮王伯伯算一下这块水稻田的面积。

演练四

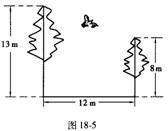
2．　 如图18-5，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞多远？