
2. 写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
[课后心得]
华师大数学课本在初二下学期,引入了函数的概念以及一次函数和反比例函数的相关性质.§18.1作为整个一章的引入课,要引导学生探索具体问题中的数量关系和变化规律,通过简单实例,了解常量、变量的意义;结合实例,了解函数的概念和三种表示方法,能举出函数的实例.
这一节的内容是较多的,而且对于今后整个一章的学习、对于同学函数观念的形成都是至关重要的.结合教材内容,根据新课程标准,我觉得在教学中要抓住学生对变量的感悟、对函数的感悟、对表达的感悟.在教学中主要围绕数量关系来刻画变化规律,借助信息技术,按照“先宏观,再微观;先粗略,再细化,再严格”的步骤来进行本课的教学.通过本课,不但要解决学生学习中可能产生的困难,更要让学生初步的体会到函数的思想方法,为扎实的掌握函数相关知识打下基础.

|
|||||||||||||||||||||||||
|

请学生根据自己的生活经验来举出一个例子,并将之表达出来.
评注:这个活动要求学生在本课前作一些准备工作.请每一位同学在课前都在预习的基础上,仿照课本上的问题,自己去身边寻找几个变量之间变化的关系,并设法记录下来.在课上请同学来讲讲自己身边的这些变化关系,分析表达的形式,变量和常量,自变量和因变量.但是同学有些可能找出来的并不是我们这里所说的函数关系,在课上要注意辩析清楚.
[小结与作业]
小节:本课主要学习了用函数的观念来分析一个变化的过程,同学在平时要多注意留意身边的现象,多尝试用数学的眼光去观察、分析.
作业:
1. 下表是某市2000年统计的该市男学生各年龄组的平均身高.

(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?
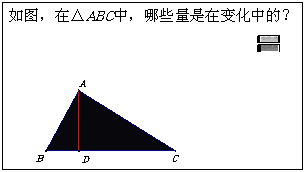
运行“04 现象.gsp”,演示效果:△ABC的高AD平移,底部BC不动.
教师:请同学们观察在屏幕上这个变化过程中,有哪些是变量?这些变量之间是否存在函数关系?如果存在函数关系,你准备用什么方法来表示这样的函数关系?
评注:这个课堂活动主要是巩固前面所学习的函数关系,学生在观察屏幕,寻找变量的过程中,自觉的运用函数的观念来看这个运动的图像,增强应用数学的意识.
从前面的几个实例中,来感受函数的各种表达方式
|
实例 |
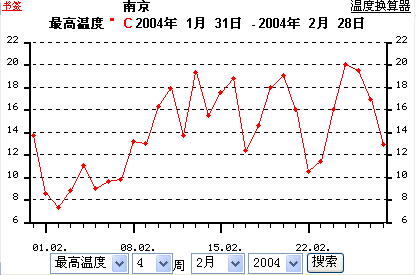
一天的温度变化 |
高尔夫球的运动 |
水中的波纹 |
|
适用的表达方式 |
图像法,列表法 |
图像法,列表法,表达式 |
列表法,表达式 |
教师:以上实例的变化过程中,都有一些数量在变化,这样的量我们称为变量.如果在过程中,保持不变的就称为常量.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
在实例1中,时间t是自变量,气温T是因变量,对于时间t的每一个值,气温T都有唯一的值与之对应,称气温T是时间t的函数.
在实例2中,水平距离l是自变量……
(以下略)
带领学生,在每一个实例中重新巩固“自变量”、“因变量”、“函数”的概念.
例1 日气温变化图
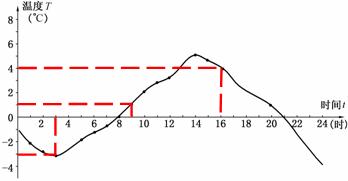 图18.1.1是某日的气温变化图.
图18.1.1是某日的气温变化图.
看图回答:
教师:根据这张图,你能否得到某个时刻的温度?
学生1:凌晨3点时,温度为零下3摄氏度.
学生2:上午7点,温度为1摄氏度.
学生3:下午4点,温度为4摄氏度.
把以上这些数据填入表格
|
时间t |
3 |
7 |
12 |
16 |
… |
|
气温T |
-3 |
1 |
3 |
4 |
… |
教师:在哪一段时间内,温度是上升的?
学生4:从凌晨3点起,到下午2点止,这期间温度是持续上升的.
教师:在这张图中,主要体现了那些数量的变化?
学生5:有温度的变化;学生6:还体现了时间的变化.
结论:从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.每一个时间t,都有一个唯一的气温T与之对应.

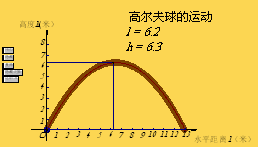 例2 高尔夫球的轨迹
例2 高尔夫球的轨迹
演示高尔夫球的动画,并将之抽象为上面右图所示的轨迹.
打开文件“2 轨迹.gsp”演示效果.
教师:我们用l标识高尔夫球飞行的水平举例,用h标识高尔夫球的飞行高度.此时高度h随着水平距离l的变化而变化.
请几位学生分别找出几组对应值,填入表格:
|
水平距离l |
2.04 |
8.20 |
… |
|
高度h |
3.35 |
5.90 |
… |
结论:随着水平距离l的变化,高度h也随之变化.每一个水平距离l都有唯一的高度h与之对应.
例3 水中的波纹
 把一块小石头投入池塘中,就会激起一阵阵的波纹.
把一块小石头投入池塘中,就会激起一阵阵的波纹.
打开文件“3 波纹.htm”演示效果.
教师:在这个图中,请同学留意哪些是在不断变化的?
学生6:水面在上下起伏.
学生7:圆的半径在不断变化.
学生8:半径的变化导致圆的面积变化,圆的周长也在变化.
打开文件“3 波纹.gsp”演示效果.
|
半径r |
1 |
2 |
3 |
4 |
… |
|
面积S |
π |
4π |
9π |
16π |
… |
结论:面积S随着半径r的变化而变化.每一个半径r都有唯一的一个面积S与之对应.
评注:考虑实例要尽量贴近学生的生活,所以对课本上提供的例子作了一些修改,最后选择了“一日内的温度变化”、“高尔夫球的运动”、“水中的波纹”这样三个例子.在上面的过程中,尽量让学生多观察,多留意在变化过程中的变量,感受“一个变量随着另一个变量的变化而变化”.
3.在某一变化过程中,可以取不同数值的量叫做变量.取值始终不变的量叫做常量.
2.表示函数关系的方法通常有三种:解析法、列表法和图象法.
1.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
8、如图4,要将楼梯铺上地毯,则需要 米的地毯。
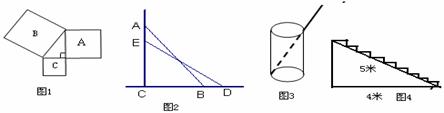
9在直角ΔABC中,斜边长为2,周长为2+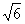 ,则ΔABC的面积为
,则ΔABC的面积为
10 △ABC中,CE是AB边上的中线,CD⊥AB于D,且AB=5,BC=4,AC=6,则DE的长为_______.
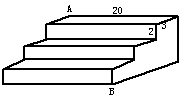
11如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是
12在△ABC中,∠C=90°,(1)已知 a=2.4,b=3.2,则c= ;(2)已知c=17,b=15,则△ABC面积等于 ;(3)已知∠A=45°,c=18,则a= .
三 解下列各题(40)
1 已知:如图,⊿ABC中,∠ACB =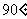 ,AB = 5cm,BC = 3 cm,CD⊥AB于D,
,AB = 5cm,BC = 3 cm,CD⊥AB于D,
 求CD的长及三角形的面积;(4分)
求CD的长及三角形的面积;(4分)
2 一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.(4分)
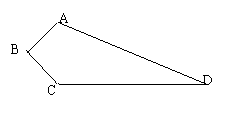 3如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AC⊥CD,AB=3m,BC=4m,,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?(5)
3如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AC⊥CD,AB=3m,BC=4m,,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?(5)
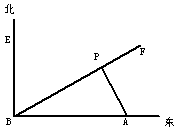
4 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域。(5)
(1) A城是否受到这次台风的影响?为什么?
(2) 若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
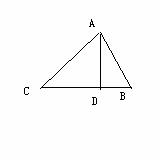
4 如图,△ABC中,AB=13,BC=14,CA=15,求BC边上的高AD(5)
,
5 有一只小鸟在一棵高4m的小树梢上捉虫子,它的伙伴在离该树12m,高20m的一棵大树的树梢上发出友好的叫声,它立刻以4m/s的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?(5)

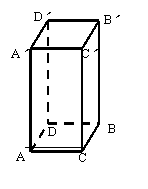 6 已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?(5)
6 已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?(5)
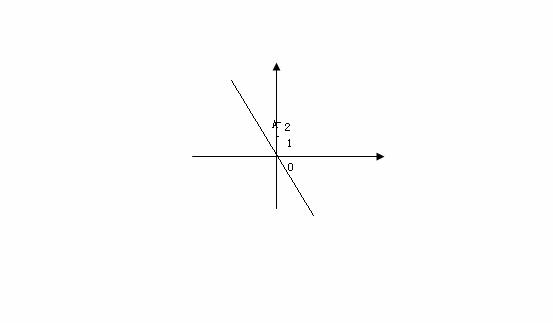
7 (2009年四川省数学竞赛题)如图,点A坐标为(0,2),在一次函数y=-2x 的图像上是否存在一点P,使P与OA构成等腰三角形,若存在
求出所有满足条件的点P的坐标,不存在说明理由。(7)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com