
2.求函数值的方法:把所给出的自变量的值代入函数解析式中,即可求出相应的函数值.
1.求函数自变量取值范围的两个依据:
(1)要使函数的解析式有意义.
①函数的解析式是整式时,自变量可取全体实数;
②函数的解析式分母中含有字母时,自变量的取值应使分母≠0;
③函数的解析式是二次根式时,自变量的取值应使被开方数≥0.
(2)对于反映实际问题的函数关系,应使实际问题有意义.
例1 求下列函数中自变量x的取值范围:(1) y=3x-1; (2) y=2x2+7;(3) ; (4)
; (4) .
.
分析 用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值.例如,在(1),(2)中,x取任意实数,3x-1与2x2+7都有意义;而在(3)中,x=-2时, 没有意义;在(4)中,x<2时,
没有意义;在(4)中,x<2时,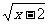 没有意义.
没有意义.
解 (1)x取值范围是任意实数;
(2)x取值范围是任意实数;
(3)x的取值范围是x≠-2;
(4)x的取值范围是x≥2.
归纳 四个小题代表三类题型.(1),(2)题给出的是只含有一个自变量的整式;(3)题给出的是分母中只含有一个自变量的式子;(4)题给出的是只含有一个自变量的二次根式.
例2 分别写出下列各问题中的函数关系式及自变量的取值范围:
(1)某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式;
(2)已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;
(3)在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式.
解 (1) y=0.50x,x可取任意正数;
(2)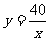 ,x可取任意正数;
,x可取任意正数;
(3)S=100π-πr2,r的取值范围是0<r<10.
例3 在上面的问题(3)中,当MA=1 cm时,重叠部分的面积是多少?
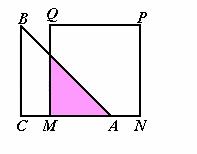
解 设重叠部分面积为y cm2,MA长为x cm, y与x之间的函数关系式为
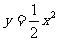
当x=1时,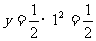
所以当MA=1 cm时,重叠部分的面积是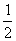 cm2.
cm2.
例4 求下列函数当x = 2时的函数值:
(1)y = 2x-5 ; (2)y =-3x2 ;
(3) ; (4)
; (4) .
.
分析 函数值就是y的值,因此求函数值就是求代数式的值.
解 (1)当x = 2时,y = 2×2-5 =-1;
(2)当x = 2时,y =-3×22 =-12;
(3)当x = 2时,y = = 2;
= 2;
(4)当x = 2时,y = = 0.
= 0.
思考 (1)在上面问题中所出现的各个函数中,自变量的取值有限制吗?如果有,写出它的取值范围.
(2)在上面问题1中,当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加数为6时,横向的加数是多少?
分析 问题1,观察加法表中涂黑的格子的横向的加数的数值范围.
问题2,因为三角形内角和是180°,所以等腰三角形的底角的度数x不可能大于或等于90°.
问题3,开始时A点与M点重合,MA长度为0cm,随着△ABC不断向右运动过程中,MA长度逐渐增长,最后A点与N点重合时,MA长度达到10cm.
解 (1)问题1,自变量x的取值范围是:1≤x≤9;
问题2,自变量x的取值范围是:0<x<90;
问题3,自变量x的取值范围是:0≤x≤10.
(2)当涂黑的格子横向的加数为3时,纵向的加数是7;当纵向的加数为6时,横向的加数是4. 上面例子中的函数,都是利用解析法表示的,又例如:
s=60t, S=πR2.
在用解析式表示函数时,要考虑自变量的取值必须使解析式有意义.在确定函数中自变量的取值范围时,如果遇到实际问题,不必须使实际问题有意义.例如,函数解析式S=πR2中自变量R的取值范围是全体实数,如果式子表示圆面积S与圆半径R的关系,那么自变量R的取值范围就应该是R>0.
对于函数 y=x(30-x),当自变量x=5时,对应的函数y的值是
y=5×(30-5)=5×25=125.
125叫做这个函数当x=5时的函数值.
问题1 填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.

解 如图能发现涂黑的格子成一条直线.
函数关系式:y=10-x.
问题2 试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式.
解 y与x的函数关系式:y=180-2x.
问题3 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式.

解 y与x的函数关系式: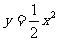 .
.
4.填写如图所示的乘法表,然后把所有填有24的格子涂黑.若用x表示涂黑的格子横向的乘数,y表示纵向的乘数,试写出y关于x的函数关系式.

3.写出下列函数关系式,并指出式中的自变量与因变量:
(1)每个同学购一本代数教科书,书的单价是2元,求总金额Y(元)与学生数n(个)的关系;
(2)计划购买50元的乒乓球,求所能购买的总数n(个)与单价a(元)的关系.
2.分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的关系式是 ;
;
(2)若直角三角形中的一个锐角的度数为α,则另一个锐角β(度)与α间的关系式是β=90-α ;
(3)若某种报纸的单价为a元,x表示购买这种报纸的份数,则购买报纸的总价y(元)与x间的关系是:y=ax.
1.举3个日常生活中遇到的函数关系的例子.
3.函数关系三种表示方法:
(1)解析法;
(2)列表法;
(3)图象法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com