
例1. 已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。
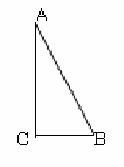
证明方法一:取四个与Rt△ABC全等的直角三角形,把它们拼成如图所示的正方形。
如图,正方形ABCD的面积 = 4个直角三角形的面积 + 正方形PQRS的面积
∴ ( a + b )2 = 1/2 ab × 4 + c2
a2 + 2ab + b2 = 2ab + c2
故 a2 + b2 =c2
证明方法二:
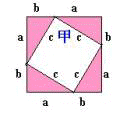
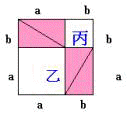
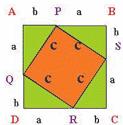
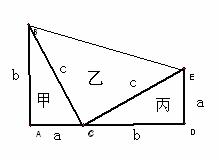
图1中,甲的面积 = (大正方形面积) - ( 4个直角三角形面积)。
图2中,乙和丙的面积和=(大正方形面积)-( 4个直角三角形面积)。
因为图1和图2的面积相等,
所以甲的面积=乙的面积+丙的面积
即:c2 = a2 + b2
证明方法三:
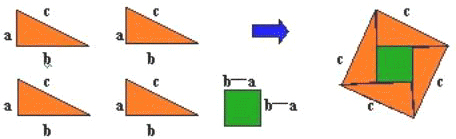
四个直角三角形的面积和 +小正方形的面积 =大正方形的面积,
2ab + ( a -b ) 2 = c2,
2ab + a2 - 2ab + b2 = c2
故 a2 + b2=c2
证明方法四:
梯形面积 = 三个直角三角形的面积和
1/2 × ( a + b ) × ( a + b ) = 2 × 1/2 × a × b + 1/2 × c × c
(a + b )2 = 2ab + c2
a 2 + 2ab + b2 = 2ab + c2
故 a2 + b2=c2
点拨:以上四种方法均是使用了面积的方法,勾股定理的证明方法很多,有四百多种,在后面学习了相似三角形之后,我们还可以用相似三角形的方法来证明。
例2. 在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a=1,c=2, 求b。
⑶已知c=17,b=8, 求a。
⑷已知a:b=1:2,c=5, 求a。
⑸已知b=15,∠A=30°,求a,c。
分析:⑴已知两直角边,求斜边直接用勾股定理。⑵⑶已知斜边和一直角边,求另一直角边,用勾股定理的变形式。⑷⑸已知一边和两边比,求未知边。

解:由a2 + b2=c2得,
(1)c2=
52 + 52=50, 即:c= ;
;
(2)12 + b2=22,b2=3,即:b=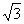 ;
;
(3)a2 + 82=172 ,a2=225,即:a=15;
(4)由a:b=1:2得,b=2a,
则:a2 + (2a)2=52
即:a=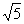 ;
;
(5)由∠A=30°得,c=2a,
则:a2 +152=(2a)2 ,
解得:a=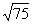 ,c=2
,c=2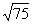 。
。
注:本题中的 、
、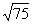 在学习二次根式之后还可以进一步化简,此处不作要求。
在学习二次根式之后还可以进一步化简,此处不作要求。
例3. 已知:如图,等边△ABC的边长是6cm。⑴求等边△ABC的边AB上的高CD。⑵求S△ABC。
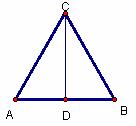
分析:等边三角形的每边上的高、中线和该边所对的角的角平分线,三线合一。
解:(1)∵△ABC 是等边三角形
CD⊥AB
∴CD平分AB
∵△ABC的边长是6cm
∴AD=BD=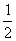 AB=3 cm
AB=3 cm
在直角三角形ACD中,
AD2+CD2=AC2
32+CD2=62
CD=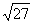
(2)S△ABC=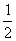 AB·CD=
AB·CD=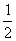 ×6×
×6×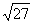 =3
=3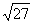 (cm2)
(cm2)
例4. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个男孩头顶5000米,飞机每小时飞行多少千米?
分析:根据题意,可以先画出符合题意的图形。如图,图中△ABC的∠C=90°,AC=4000米,AB=5000,米欲求飞机每小时飞行多少千米,就要知道20秒时间里飞行的路程,即图中的CB的长,由于△ABC的斜边AB=5000米,AC=4000米,这样BC就可以通过勾股定理得出,这里一定要注意单位的换算。

解:由勾股定理得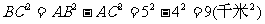
即 BC=3千米
飞机 20秒飞行3 千米.那么它 l 小时飞行的距离为:
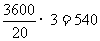 (千米/时)
(千米/时)
答:飞机每小时飞行 540千米。
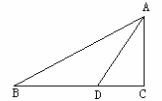
例5. 如图在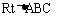 中,
中,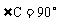 ,
,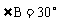 ,
,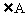 的平分线AD交BC于D,求证:
的平分线AD交BC于D,求证: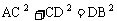 。
。
证明: ,
,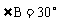
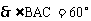
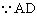 平分
平分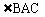
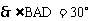
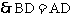
在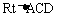 中
中
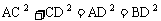
点评:本题是一道勾股定理的运用题,在本题中我们也用到了角平分线的知识。
例6. 如图,在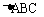 中,
中,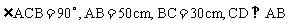 于D,求CD的长。
于D,求CD的长。
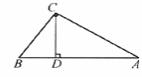
解: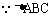 是直角三角形
是直角三角形
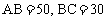 ,由勾股定理有
,由勾股定理有
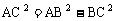
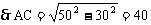
又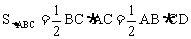
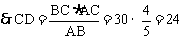
答:CD的长是24cm。
点评:(1)勾股定理的应用前提是在直角三角形中;(2)本题求CD也可以分别在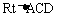 和
和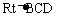 中用勾股定理列方程组
中用勾股定理列方程组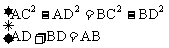 来求解,显然解方程需要以后的知识而且比用面积法繁杂些。
来求解,显然解方程需要以后的知识而且比用面积法繁杂些。
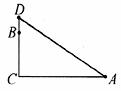
例7. 在一棵树的10m高的B处有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只爬到树顶后直接跃向池塘的A处,如果两只猴子所经过的距离相等,试问这棵树有多高?
分析:如图所示,其中一只猴子从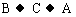 共30m,另一只猴子从
共30m,另一只猴子从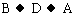 也共走了30m。并且树垂直于地面,于是此问题可化归到直角三角形解决。
也共走了30m。并且树垂直于地面,于是此问题可化归到直角三角形解决。
解:如图,设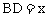 ,由题意知
,由题意知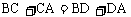
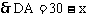
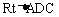 中,
中,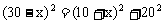 ,解之得
,解之得
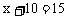
答:这棵树高15m。
点评:本题的关键是依题意正确地画出图形,在此基础上,再运用勾股定理及方程的思想使问题得以解决。
[模拟试题](答题时间:45分钟)
4. 勾股定理的各种表达式
在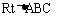 中,
中,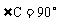 ,
,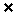 A、
A、 B、
B、 C的对边分别为a、b、c,则
C的对边分别为a、b、c,则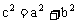 ,
,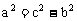 ,
,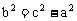 ,
, ,
,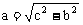 ,
,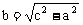 。
。
3. 勾股定理的作用:
1)已知直角三角形的两边长,求第三边长;
2)知道一边长时,能够确定直角三角形的其余两个边长之间的关系;
3)在证明含平方问题时,有时就可以考虑构造直角三角形帮助解决问题。
2. 相关知识链接:
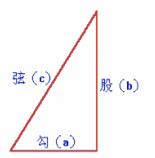
直角三角形
1)我国古代把直角三角形中较短的直角边叫作勾,较长的直角边叫作股,斜边叫作弦;
2)汉代数学家赵爽把勾股定理叙述成:勾股各自乘,并之为弦实,开方除之即弦;
3)国外称之为毕达哥拉斯定理;
4)也有人称勾股定理为千古第一定理。
1. 定理内容:
文字形式:直角三角形的两直角边的平方和,等于斜边的平方。
几何形式:如果直角三角形的直角边分别为a、b,斜边为c,那么
a2+b2=c2
2. 难点:勾股定理的证明和运用;
1. 重点:勾股定理的内容
4. 能够运用勾股定理解决相关问题。
3. 会用面积法来证明勾股定理;
2. 理解勾股定理的含义;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com