
3.已知等腰三角形的周长为12cm,若底边长为y cm,一腰长为x cm.
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围;
(3)画出这个函数的图象.
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).

1.下图为世界总人口数的变化图.根据该图回答:
(1)从1830年到1998年,世界总人口数呈怎样的变化趋势?
(2)在图中,显示哪一段时间中世界总人口数变化最快?

2.在观察实际问题的图象时,先从两坐标轴表示的实际意义得到点的坐标的实际意义.然后观察图形,分析两变量的相互关系,给合题意寻找对应的现实情境.
1.画实际问题的图象时,必须先考虑函数自变量的取值范围.有时为了表达的方便,建立直角坐标系时,横轴和纵轴上的单位长度可以取得不一致;
例1 王强在电脑上进行高尔夫球的模拟练习,在某处按函数关系式 击球,球正好进洞.其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
击球,球正好进洞.其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
(1)试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?
分析 (1)高尔夫球飞行的路线,也就是函数 的图象,用描点法画出图象.在列表时要注意自变量x的取值范围,因为x是球飞出的水平距离,所以x不能取负数.在建立直角坐标系时,横轴(x轴)表示球飞出的水平距离,纵轴(y轴)表示球的飞行高度.
的图象,用描点法画出图象.在列表时要注意自变量x的取值范围,因为x是球飞出的水平距离,所以x不能取负数.在建立直角坐标系时,横轴(x轴)表示球飞出的水平距离,纵轴(y轴)表示球的飞行高度.
(2)高尔夫球的最大飞行高度就是图象上函数值y取最大值的点,如图点P,点P的纵坐标就是高尔夫球的最大飞行高度;球的起点与球进洞点是球飞出的水平距离最小值的点和最大值的点,如图点O和点A,点O和点A横坐标差的绝对值就是球的起点与洞之间的距离.
解 (1)列表如下:

在直角坐标系中,描点、连线,便可得到这个函数的大致图象.

(2)高尔夫球的最大飞行高度是3.2 m,球的起点与洞之间的距离是8 m.
例2 小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.请你由图具体说明小明散步的情况.

分析 从图中可发现函数图象分成四段,因此说明小明散步的情况应分成四个阶段.
线段OA:O点的坐标是(0,0),因此O点表示小明这时从家里出发,然后随着x值的增大,y值也逐渐增大(散步所用时间越长,离家的距离越大),最后到达A点,A点的坐标是(3,250),说明小明走了约3分钟到达离家250米处的一个阅报栏.
线段AB:观察这一段图象可发现x值在增大而y值保持不变(小明这段时间离家的距离没有改变),B点横坐标是8,说明小明在阅报栏前看了5分钟报.
线段BC:观察这一段图象可发现随着x值的增大,y值又逐渐增大,最后到达C点,C点的坐标是(10,450),说明小明看了5分钟报后,又向前走了2分钟,到达离家450米处.
线段CD:观察这一段图象可发现随着x值的增大,而y值逐渐减小(10分钟后散步所用时间越长,离家的距离越小),说明小明在返回,最后到达D点,D点的纵坐标是0,表示小明已到家.这一段图象说明从离家250米处返回到家小明走了6分钟.
解 小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家.
看上面问题的图,回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
分析 (1)小强让爷爷先跑的路程,应该看表示爷爷的这条线段.由于从小强开始爬山时计时的,因此这时爷爷爬山所用时间是0,而x轴表示爬山所用时间,得x=0.可在线段上找到这一点A(如图).A点对应的函数值y=60.
(2) y轴表示离开山脚的距离,山顶离山脚的距离指的是离开山脚的最大距离,也就是函数值y取最大值.可分别在这两条线段上找到这两点B、C(如图),过B、C两点分别向x轴、y轴作垂线,可发现交y轴于同一点Q(因为两人爬的是同一座山), Q点的数值就是山顶离山脚的距离,分别交x轴于M、N,M、N点的数值分别是小强和爷爷爬上山顶所用的时间,比较两值的大小就可判断出谁先爬上山顶.

解 (1)小强让爷爷先上60米;
(2)山顶离山脚的距离有300米,小强先爬上山顶.
归纳 在观察实际问题的图象时,先从两坐标轴表示的实际意义得到点的坐标意义.如图中的点P(3,90),这一点表示小强爬山3分后,离开山脚的距离90米.再从图形中分析两变量的相互关系,寻找对应的现实情境.如图中的两条线段都可以看出随着自变量x的逐渐增大,函数值y也随着逐渐增大,再联系现实情境爬山所用时间越长,离开山脚的距离越大,当x达到最大值时,也就是到达山顶.
问题 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).

问 图中有一个直角坐标系,它的横轴(x轴)和纵轴(y轴)各表示什么?
答 横轴(x轴)表示两人爬山所用时间,纵轴(y轴)表示两人离开山脚的距离.
问 如图,线段上有一点P,则P的坐标是多少?表示的实际意义是什么?
答 P的坐标是(3,90).表示小强爬山3分后,离开山脚的距离90米.
我们能否从图象中看出其它信息呢?
5.画出下列函数的图象:
(1)y=4x-1; (2)y=4x+1.
4.(1)画出函数 的图象(在-4与4之间,每隔1取一个x值,列表;并在直角坐标系中描点画图).
的图象(在-4与4之间,每隔1取一个x值,列表;并在直角坐标系中描点画图).
(2)判断下列各有序实数对是不是函数 的自变量x与函数y的一对对应值,如果是,检验一下具有相应坐标的点是否在你所画的函数图象上:
的自变量x与函数y的一对对应值,如果是,检验一下具有相应坐标的点是否在你所画的函数图象上:
 ,
, ,(-1,3),
,(-1,3),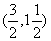 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com