3.(1)画出函数y＝2x－1的图象(在－2与2之间，每隔0.5取一个x值，列表；并在直角坐标系中描点画图)．

(2)判断下列各有序实数对是不是函数y＝2x－1的自变量x与函数y的一对对应值，如果是，检验一下具有相应坐标的点是否在你所画的函数图象上：

(－2.5,－4)，(0.25,－0.5)，(1,3)，(2.5,4)．

2.画出函数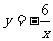的图象(先填写下表，再描点、然后用光滑曲线顺次连结各点)．

1.在所给的直角坐标系中画出函数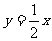的图象(先填写下表，再描点、连线)．

3.连线：按照自变量由小到大的顺序，把所描各点用光滑的曲线连结起来．

描出的点越多，图象越精确．有时不能把所有的点都描出，就用光滑的曲线连结画出的点，从而得到函数的近似的图象．

2.描点：以表中对应值为坐标，在坐标平面内描出相应的点；

由函数解析式画函数图象，一般按下列步骤进行：

1.列表：列表给出自变量与函数的一些对应值；

例1 画出函数y＝x+1的图象．

分析 要画出一个函数的图象，关键是要画出图象上的一些点，为此，首先要取一些自变量的值，并求出对应的函数值．解 取自变量x的一些值，例如x＝－3，－2,－1，0，1，2，3 …，计算出对应的函数值．为表达方便，可列表如下：

由这一系列的对应值，可以得到一系列的有序实数对：

…，(－3,－2)，(－2,－1)，(－1,0)，(0,1)，(1,2)，(2,3)，(3,4)，…在直角坐标系中，描出这些有序实数对(坐标)的对应点，如图所示．

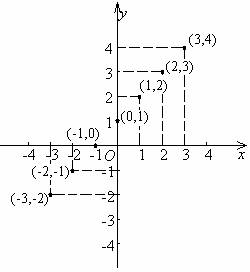
通常，用光滑曲线依次把这些点连起来，便可得到这个函数的图象，如图所示．

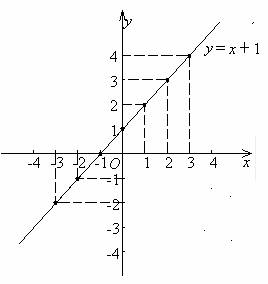
这里画函数图象的方法，可以概括为列表、描点、连线三步，通常称为描点法．

例2 画出函数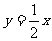的图象．

分析 用描点法画函数图象的步骤：分为列表、描点、连线三步．

解 列表：

描点：

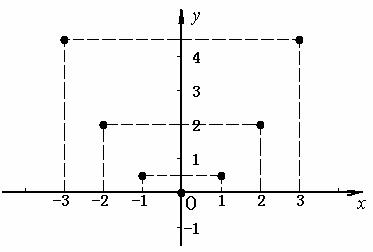
用光滑曲线连线：

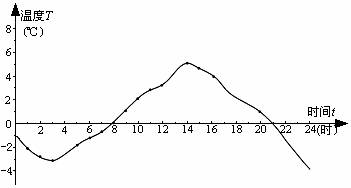
先考虑一个简单的问题：你是如何从图上找到各个时刻的气温的？

分析 图中，有一个直角坐标系，它的横轴是t轴，表示时间；它的纵轴是T轴，表示气温．这一气温曲线实质上给出了某日的气温T (℃)与时间t(时)的函数关系．例如，上午10时的气温是2℃，表现在气温曲线上，就是可以找到这样的对应点，它的坐标是(10,2)．实质上也就是说，当t＝10时，对应的函数值T＝2．气温曲线上每一个点的坐标(t,T)，表示时间为t时的气温是T．

问题2 如图,这是2004年3月23日上证指数走势图，你是如何从图上找到各个时刻的上证指数的？

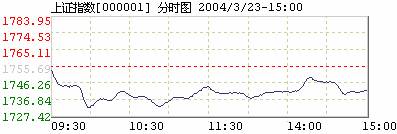
分析 图中，有一个直角坐标系，它的横轴表示时间；它的纵轴表示上证指数．这一指数曲线实质上给出了3月23日的指数与时间的函数关系．例如，下午14:30时的指数是1746.26，表现在指数曲线上，就是可以找到这样的对应点，它的坐标是(14:30, 1746.26)．实质上也就是说，当时间是14:30时，对应的函数值是1746.26．

上面气温曲线和指数走势图是用图象表示函数的两个实际例子．

一般来说，函数的图象是由直角坐标系中的一系列点组成的图形．图象上每一点的坐标(x，y)代表了函数的一对对应值，它的横坐标x表示自变量的某一个值，纵坐标y表示与它对应的函数值．

问题1 在前面，我们曾经从如图所示的气温曲线上获得许多信息，回答了一些问题．现在让我们来回顾一下．

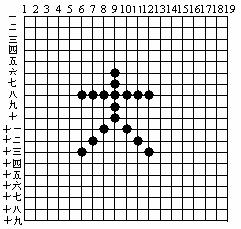
5.如图是一个围棋棋盘，我们可以用类似于直角坐标系的方法表示各个棋子的位置．例如，图中右下角的一个棋子可以表示为(12,十三)．请至少说出图中四个棋子的“位置”．